Analysis of the Efficiency of Traffic Control Algorithms on the Vanderbilt Campus

ABSTRACT

Traffic Signal Control (TSC) has been a very important venue of research for many years. More recently, traffic as a whole has been experimented with using various traffic simulations, one being the Simulation of Urban Mobility (SUMO), in which testing TSC in particular is possible. In addition to SUMO, a data set called RESCO benchmark was used, with, among other things, to change the TSC algorithm that is being used for all the intersections, thus changing the behavior of the simulation. Using this program and the RESCO benchmark, I conducted experiments using the Stochastic method, the MaxWave method, and the MaxPressure method (all these algorithms originate with the RESCO benchmark) on a traffic network in Nashville, TN near Vanderbilt University. These experiments showcased that traffic signals using the Stochastic method caused much more traffic congestion and wait times than both the MaxWave and MaxPressure methods.

INTRODUCTION.

Traffic Signal Control (TSC) is the process of managing and coordinating different traffic lights. Traffic lights at intersections are managed in phases. Phases are counted in the order they go, with the first phase being 1, second being 2, etc. At the bare minimum, every traffic light in an intersection is coordinated with each other. For example, Figure 1 below shows that there are a set number of phases when each traffic light in an intersection displays its signal at different times within the phase count. This is because it is impossible to have all cars go at once, so the different wait times need to be strictly regulated, so that cars can travel along their routes safely without any incidents.

TSC is imperative for the orderly operation of traffic in modern urban environments. The big reason for this is because it manages the order in which the different traffic movements can happen. Managing traffic this way helps prevent crashes and makes it possible for traffic to flow much smoother and more efficiently. In addition, traffic signals must be clear and easy to understand for all vehicles involved in traffic intersections, lest a crash occur.

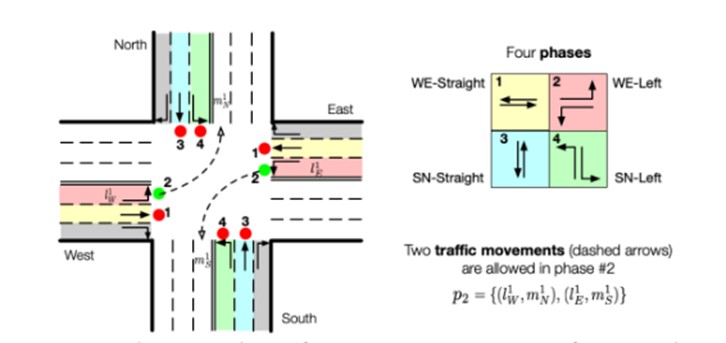
There are numerous approaches to solving these problems, but ones that are commonly used for comparison in research are the Stochastic, the MaxWave, and the MaxPressure methods. [2] The Stochastic method simply follows the predetermined phase order: it goes from phase 1, to phase 2, to phase 3, then back to phase 1. As for MaxWave, it considers whichever phase has the largest number of cars that have been backed up, and then lets that phase go first. MaxPressure does the same thing as MaxWave, but instead it considers how letting one phase go will impact other intersections. For instance, if letting the phase with the largest number of cars backed up first causes even more traffic at the other intersections, another queue will be allowed to go before it. To study TSC, we use simulation environments. For example, a program called Simulation of Urban Mobility (SUMO) is popular. Other simulators that are used include AIMSUN, CORSIM, and MATsim [3, 4, 5].

SUMO was used to collect all the data in this article. However, in SUMO, the algorithms that were mentioned above are not included in the software, so they must be externally coded. For this, I used a software library called RESCO benchmark [2]. This benchmark was coded with Python, and I edited this code to fit the map scenarios.

In this paper, I compared the different algorithms, Stochastic, MaxWave, and MaxPressure, to one another. I created three different demand scenarios and tested each algorithm on them. A demand scenario defines the different movements of cars within the scenario, i.e., the timing, the number, and the direction the cars go through the scenario. This created 9 experiments in total. A major contribution of my work comes in the scenario I modeled, which was the area around Edgehill Avenue near the Vanderbilt University building in which I conducted my research. This contribution is notable because there has never been a research paper for SUMO done in this stretch of road before and with those specific demand structures arranged in such a way.

MATERIALS AND METHODS.

This paper tests several traffic algorithms for traffic signal control on a section of road that is near Vanderbilt University. The OSM (Open Street Map) web wizard [6] was used to create a traffic scenario and then to test algorithms on the scenarios. These algorithms were measured using different demand scenarios, which provided insight to how these traffic algorithms would behave when the demands in the area were changed. These algorithms changed how the traffic light intersections behaved, and studying this was very important for the data that was gathered/collected because knowing which traffic algorithm is the best can help save vehicle drivers’ time. To be able to use the algorithms, RESCO benchmark [2] is used to test the different demand scenarios. The RESCO benchmark is coded in Python. Python is used for running the algorithms, and to do that effectively, it is required inputting each phase directly into Python – when defining a new scenario, all the phases are required to be documented within the Python script and in the new scenario that was built within it.

Creating Scenario.

The first step to model the scenario used the OSM web wizard [2], a program in which you can take a snapshot of a section of road, which then will import this into SUMO. After, SUMO can be used to run a simulation of the road and the cars in it, in which all the cars will move through the scenario, and after their movements finish, the time it took will be displayed, and then data can be gathered from the scenario. However, if further editing is required or wanted (this is almost always the case), then the scenario must be moved into a program called NETedit. In NETedit, a user can edit tiny parts of the scenario, such as the edges (the individual traffic lanes) and the demands (the several cars in the scenario). Additionally, within NETedit, Traffic Assignment Zones (TAZs) can be created, which are areas in which vehicles can enter and then exit the scenario. Along with TAZs, vehicles can also enter or exit along edges that are at the end of the simulation. Once the demand exits the scenario, the car is no longer simulated within the scenario and is no longer visible. Edges are lanes of traffic that demands run on, and that connect the junctions to one another. Furthermore, editing the junctions (intersections) with traffic lights is important, so I can edit the specific phases of each traffic light. After these steps have been completed, I can save the program and then run it again in SUMO. In this research, a scenario was created (see Figure 2) based on the section of the campus that was near the building that I worked, which is in an area around the Vanderbilt campus (Figure 3). NETedit is an important part of this whole process that must be delved into further. The basic ‘building blocks’ of NETedit consist of what are called junctions and edges. Junctions include intersections but can also simply include where consecutive edges meet at, such as the midpoint between two sections of road(edges). Junctions can be made into priority, traffic lights, 4 way stops, and many other intersection types. Edges can be made into traditional 2 lane roads (one going each direction) or multiple lanes going in the two directions.

 

Demand Patterns.

Next, I added the different vehicles (referred to as demands) to the scenario. There are either flows (multiple cars along the same route in a long period of time) or singular cars traveling on a single route from the exit to the entrance. To create wide areas of demand entry into the simulation, a TAZ is needed. I created the TAZs to run different routes around the map, starting an ending at different TAZs. After this, I saved the demand and route files as XML files, and a SUMO file, to run in the SUMO program itself.

Each demand scenario is different from one another, and they have been created to model different things. The first scenario, NEUTRAL, has a small number of traffic flows and is intended to model a large amount of traffic, originating from a small amount of TAZs that cover many edges within the scenario. This demand scenario is the most basic of the three. The second demand scenario, called CROSS, has a roughly equal number of cars going from which corner they start to their direct diagonal corner (the TAZ), for example, starting from northeast TAZ and heading to, and exiting from, the southwest TAZ. The third demand scenario, REALISTIC, aims to give the traffic a more realistic feel, with it including many different flows of where traffic, coming from different TAZs, can move and flow from, while weighing more ‘realistic’ flows and deprioritizing ‘less realistic’ flows, as opposed to CROSS, which had every minor flow (besides the main large flow down on Edgehill, all flows are from one TAZ to another) be equal in number of demands.

Algorithms.

In this paper I compared three different algorithms, Stochastic, MaxWave, and MaxPressure. First, stochastic runs each of the traffic phases in their original order without change. So, it would go to phase 1, phase 2, phase 3 and so on. MaxWave, on the other hand, says that for whatever phase of traffic has the greatest number of cars backed up, it will let that phase go, then the phase with the second the greatest number of cars, then so on. MaxPressure [7] states the same, but it takes into consideration the adjacent intersections to the current intersection in question, and if there is a lot of blockages in an adjacent intersection, it lets whichever phase has the most amount of traffic built up that does not lead to additional traffic.

I created three different demand scenarios (routes for cars to travel on) and tested each algorithm on each demand scenario. This created 9 experiments in total that were to be simulated.

There was a part of this that was unique – the scenario I created was the area around Edgehill Avenue, specifically near the Vanderbilt University building in which I conducted my research. Modeling this specific stretch of road had never been tested before, and this new direction adds to the TSC literature in a way that has never been accomplished before. Furthermore, adding in the new and specific demand structures to compliment the scenario I created was also unique and novel.

RESCO Benchmark.

To create data for these scenarios, an open-source benchmark called RESCO was used to run the different traffic algorithms. These algorithms were coded in the RESCO benchmark using Python. Since I created a new scenario, referred to as Nashville1, I was required to import that scenario into the Benchmark. I incorporated 5 different traffic light intersections, in which for the three experiments that were run, each of them had a different traffic algorithm. The RESCO benchmark does a multitude of things, chiefly introducing reinforcement learning into SUMO, but the thing that I focused on in my research was the part which determined what the different traffic signals did and how they interacted with one another. As mentioned above, the three individual algorithms were called the Stochastic method, the MaxWAVE method, and the MaxPressure method.

RESULTS.

Efficiency of the algorithms and demand scenarios were measured using two different metrics. These metrics are called Average Vehicle Delay and Average Speed. Average Vehicle Delay measures the average amount of ‘extra’ time that a vehicle spends in the simulation. This is relative to the amount of time a car would spend in a scenario without any barriers (traffic jams, red lights, etc). The second metric that was used is called the average vehicle speed. This measures the average speed that vehicles will travel through the scenario at.

As for the first metric, Average Speed is calculated using the average of the speed of all cars in the simulation. This calculates the speed of all vehicles in the simulation, where N is the total number of cars, while  is the average speed of the nth car.

\[average\ speed=\frac{1}{n}\sum_{n=1}^{N}{\underline{v}}_n\tag{1}\]

The second metric, which is Average Vehicle delay, showcases the difference between the actual travel time and the minimum possible travel time that is possible. The minimum amount of time is usually different from the actual travel time since obstacles that require the car to slow down are present, such as stop lights, other vehicles, or pedestrians. The average delay metric calculates the mean delay over all the vehicles in the simulation.

\[average\ delay=\frac{1}{N}\sum_{n=1}^{N}L_n/{\underline{v}}_n+\frac{L_n}{{V^*}_n}\tag{2}\]

The results of these experiments were quite varied. Using the average vehicle delay measured in seconds, we got the results displayed in Figure 4. [7]

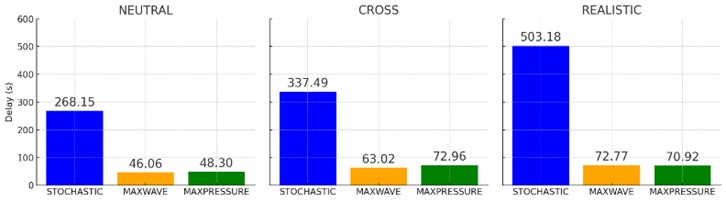
Figure 4 shows that, for all three of the demand scenarios, the stochastic has the largest amount of vehicle delay, from car to car. However, the variation between MaxPressure and MaxWave is small, but existent. For these experiments, MaxPressure and MaxWave have roughly the same effect on each traffic simulation as a whole. While MaxPressure and MaxWave have about the same vehicle delay in scenarios 2 and 3, scenario 1’s delay is much lower, which, through averaging demand scenario CROSS, results in (when MaxWave and MaxPressure are averaged and subtracted from stochastic) 220.97 seconds lost, scenario 2 loses 269.5 seconds, and scenario 3 loses a whopping 431.54 seconds. After calculating the average delay measurements, we calculated the average vehicle speed, the results of which are shown in Figure 5.

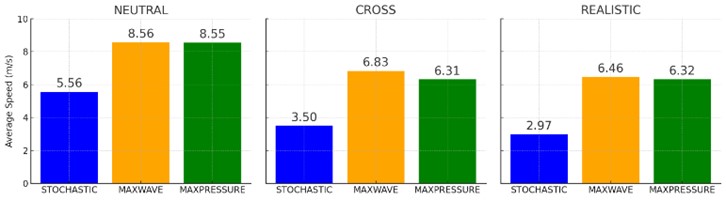
Figure 5 shows that for the stochastic method, cars will move much slower than with the other two methods. Furthermore, the three plots showcase that for all three scenarios, MaxPressure and MaxWave are roughly the same. While scenario 2 and 3’s speeds are comparable, scenario 1’s vehicles are much faster than the other two scenarios, with scenario 1’s vehicles being 7.557 m/s, while scenario 2 has an average of 5.547 m/s, while scenario 3 has an average of 5.25 m/s.

DISCUSSION.

Each of the different demand scenarios represents different ways in which traffic flows. For example, one scenario could represent traffic at 12 am, and another at 5 pm. On the other hand, for the algorithms, each of the algorithms controls traffic lights differently, and because of this, various patterns/results in the traffic simulations occur using each algorithm and each demand scenario.

Consider Demand Scenario NEUTRAL, which is the first scenario. This scenario had, compared to the others, a high average speed, and a low delay time. As was expected, the stochastic method had a much lower average speed and a much higher delay time than either MaxWave or MaxPressure. This is the case due to the very nature of the MaxPressure and MaxWave algorithms being much more efficient than the stochastic algorithm. This scenario, however, was very simple having only a couple traffic flows going in basic directions-only around three intersections that were typically used. This scenario was aimed to be a sort of a prototype. It cannot be used in real life; it is too basic and predictable.

As for the second demand scenario (Demand scenario CROSS), this scenario involved many different flows of traffic in and around as many routes as possible, but it was designed to ensure that the flows of each of these routes were evenly distributed. This led to similar results as the first scenario, with stochastic having a very large traffic delay and having a slower average speed. However, what was interesting is that for traffic delay, MaxPressure had a longer wait time, and MaxWave a shorter one, while MaxWave also had a faster average speed compared to Max Pressure for this metric. I found this to be odd, since MaxPressure is the same as MaxWave aside from it attempting to lessen traffic congestion further. I conjecture that there may be a couple possible reasons for this discrepancy. First, this discrepancy may be just due to sampling bias: due to the limitations of the testing software, not a large number of tests were run for each algorithm and demand scenario (for example, Demand scenario REALISTIC with MaxWave was run 10 times). The other explanation that I have come up with is that the part of MaxPressure that keeps the cars that are in long flows from moving if they might cause traffic congestion they will not be allowed to move. This could be causing this, as those cars will probably have a longer time spent in the scenario, and thus actually increase rather than decrease delay time.

The third scenario (Demand Scenario 2) was very similar to the second, but the number of cars in each flow were not randomly distributed. The results were similar to the second scenario, but with a smaller difference between MaxWave and MaxPressure for the two metrics, as well as the stochastic method had a much lower average speed and a much higher average vehicle delay, which was probably due to the more chaotic nature of Demand scenario REALISTIC compared to the previous two. Besides this, there is no difference between Demand scenario CROSS and Demand Scenario 2. These results surprised me because I thought that there might be a greater difference between the two, as I believed making the scenario more chaotic would change things greatly.

In summary, each of the scenarios had an overall general effect. For example, the Demand scenario NEUTRAL is the most efficient, because the cars were able to travel the fastest while experiencing the least amount of delay. However, this scenario is largely unrealistic, so it cannot be used as a means of real-world experimentation; it is a basic prototype. The other two scenarios yielded roughly the same results, with some minor differences.

More granularly, each of the findings show something different about each scenario. As for the second and third scenarios, I was surprised that they revealed such similar results. Demand scenario CROSS had an even amount of traffic flows (the same number of cars in each flow) going in many directions, while Demand scenario REALISTIC had a varied number of cars going in different directions. However, both scenarios were meant to hit as many traffic intersections as possible.

The small difference between the second and third demand scenarios and the small difference between the MaxWave and MaxPressure algorithms were unexpected. Therefore, in the future, I would like to explore this further, using mainly these two variables, on more detailed or realistic demand scenarios to see what the true difference is between MaxWave and MaxPressure, or if there really is none.

ACKNOWLEDGMENTS.

Special thanks to Dr Pamela Popp, as well as everyone at the Institute for Software Integrated Systems for helping and supporting me to do this complex and hard work.

REFERENCES

1. Wei, C. Chen, G. Zheng, K. Wu, V. Gayah, K. Xu, Z. Li, Presslight: Learning max pressure control to coordinate traffic signals in arterial networks. Proceedings of the 25th ACM SIGKDD international conference on knowledge discovery & data mining, 1290-1298 (2019)
2. Ault, G. Sharon, Reinforcement learning benchmarks for traffic signal control. Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track, (2021)
3. Barceló, J. Casas. Dynamic network simulation with AIMSUN. Simulation approaches in transportation analysis: Recent advances and challenges, 57-98 (2005).
4. Halati, H.Lieu, S. Walker. CORSIM-corridor traffic simulation model. Traffic Congestion and Traffic Safety in the 21st Century: Challenges, Innovations, and Opportunities, USDOT.., (1997).
5. W. Axhausen, A. Horni, K. Nagel. The multi-agent transport simulation MATSim. 216 (2016).
6. Krajzewicz, J. Erdmann, M. Behrisch, L. Bieker, Recent development and applications of SUMO-Simulation of Urban MObility. International journal on advances in systems and measurements, (2012)
7. Varaiya, Max pressure control of a network of signalized intersections. Transportation Research Part C: Emerging Technologies36 ,177-195 (2013)

---

---

Posted by buchanle on Friday, June 20, 2025 in May 2025.

Tags: algorithm, Demand Scenario, RESCO benchmark, simulation, Traffic Signal Control