Effective Learning of 3D Object Detection Models
ABSTRACT
This paper investigates the use of Convolutional Neural Networks (CNNs) for object detection and classification of 3D shapes from a dataset, with a focus on optimizing model performance through architectural and hyperparameter adjustments. Various modifications were applied to the CNN, including altering the number of layers, adjusting kernel sizes, modifying dropout rates, and removing Batch Normalization layers. Experimental results demonstrated that an optimal dropout rate of 0.1 maintained high accuracy, while kernel sizes of 5 were most effective for feature extraction. Removing Batch Normalization drastically reduced accuracy to 25 percent, revealing its critical role in stabilizing learning. The study highlights the importance of tuning CNN parameters for achieving robust and accurate classification in 3D shape recognition tasks. These insights provide a foundation for future work in optimizing deep learning models for complex 3D object classification challenges.
INTRODUCTION.
Convolutional Neural Networks (CNNs) have revolutionized computer vision, particularly in image classification and object detection. Inspired by the human visual system, CNNs have become essential for recognizing patterns and features in images, playing a pivotal role in applications such as autonomous vehicles, medical imaging, and augmented reality. Since the introduction of AlexNet in 2012, CNN architectures have rapidly evolved, achieving state-of-the-art performance in tasks that involve multi-category object detection and classification [10].
While CNNs are powerful due to their hierarchical feature extraction capabilities, there remains a challenge in designing networks that are both efficient and effective for specific tasks. One prominent area of research focuses on recognizing and differentiating specific components within an image—such as objects, shapes, or colors—at various levels of detail [11, 12]. Architectures such as AlexNet [10] and ResNet [14] demonstrated the benefits of deep learning with ReLU activations, max pooling, and skip connections for extracting and processing fine-grained information. Other models like VGGNet [13] and YOLO [15] further improved precision and speed, particularly in tasks that require localization of multiple parts in a single pass.
This research addresses the challenge of balancing efficiency and effectiveness by systematically evaluating different CNN architectures on a dataset of 3D shapes. By experimenting with various layers and architectural modifications, the study aims to clarify trade-offs between model accuracy, computation cost, and generalization—factors crucial for specialized applications like warehouse robotics or medical diagnosis. These insights help guide the design of future networks tailored for efficient 3D object recognition.
KEY TERMINOLOGY.
A CNN typically consists of several types of layers, each playing a critical role in the network’s ability to learn and recognize patterns in images. The key layers are: convolutional layers, which apply filters to detect features in the input image; activation layers (like ReLU), which introduce non-linearity; pooling layers, which reduce spatial dimensions and extract dominant features; fully connected layers, which perform high-level reasoning based on the extracted features; and an output layer, which produces the final prediction or classification. Additionally, CNNs may incorporate normalization layers to stabilize learning, dropout layers to prevent overfitting, and various other specialized layers depending on the specific architecture and task at hand. The following sections will discuss these layers in more detail. A schematic overview of this architecture is shown in Figure 1, which is based on canonical models like AlexNet [10].
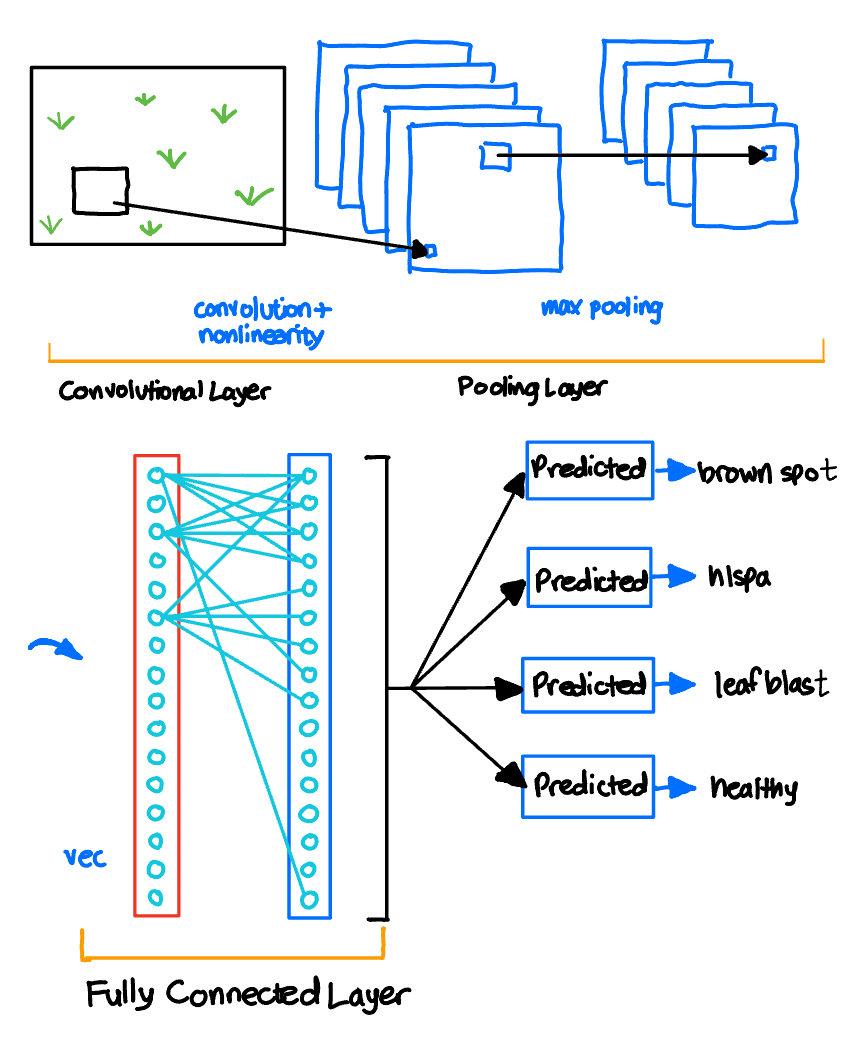
Convolutional layers.
Convolutional layers are essential components of CNNs, performing convolution operations on input data using learnable filters (kernels) to detect features like edges, textures, and shapes. These layers learn spatial hierarchies by sliding filters over the input and performing element-wise multiplications followed by summation. The resulting feature maps are combined through multiple layers to form more complex patterns. CNN architectures such as those in Krizhevsky et al.’s AlexNet [10] and subsequent models like ResNet [14] and VGGNet [13] rely heavily on these layers to capture increasingly abstract representations of visual features.
Conv2D layers, specifically designed for two-dimensional data like flat images, take a 3D tensor as input (height, width, channels) for RGB images or (height, width, 1) for grayscale images [1]. The kernel in Conv2D is a 2D matrix of weights (e.g., 3×3 or 5×5) applied to each channel [2]. As the 2D kernel moves across the input, it creates a 2D activation map representing detected features.
Mathematically, for an input image I and a kernel K, the 2D convolution operation can be expressed as Eq. 1 where * denotes the convolution operation, and (i, j) represents the position in the output feature map.
\[(I\ast K)(i,j)=\sum_{m}\sum_{n}{I(m,n)K(i-m,j-n)}\tag{1}\]
Conv2D layers reduce parameter count via sharing, enabling spatial invariance where features are detected regardless of position [3]. They support hierarchical feature learning, capturing more abstract features in deeper layers, making them effective for tasks like image classification and object detection [4].
Pooling layers.
Pooling layers, typically placed after convolutional layers, reduce the dimensionality of the data by summarizing the features within regions of the image, which helps in making the model more computationally efficient and less sensitive to small shifts or distortions in the input data. Architectures like VGGNet [13] and various object recognition systems have long utilized max pooling to preserve key spatial information while reducing computation. Although some recent models have experimented with removing pooling layers altogether [12], max pooling remains widely used due to its simplicity and its mimicry of biological vision processes.
Fully connected layers.
Finally, the fully connected layers at the end of the network take the high-level features extracted by the convolutional and pooling layers and use them to make predictions. This could be anything from identifying an object in an image to classifying it into one of several categories. CNNs have proven highly effective in a variety of applications, including image and video recognition, medical image analysis, and even natural language processing tasks. These layers are especially crucial in models like YOLO and Mask R-CNN [15, 16], where the network must output decisions based on a combination of spatial and contextual features.
Dropout and Linear Layers.
In CNNs, linear layers (also called fully connected layers) are used after the convolutional and pooling layers to learn complex patterns by connecting every neuron from the previous layer to each neuron in the current layer, effectively capturing higher-level features for classification or regression tasks. Dropout is a regularization technique used to prevent overfitting in neural networks by randomly “dropping out” a fraction of the neurons during training, which forces the network to learn more robust and generalizable features by not relying on any single neuron or path for making predictions. This technique has been particularly effective in deeper models such as those developed for the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) [10].
Batch Normalization.
Batch Normalization (BatchNorm) is a technique introduced to address the internal covariate shift problem in deep neural networks, thereby improving the stability and performance of these networks [5]. The internal covariate shift refers to the change in the distribution of network activations due to the change in network parameters during training. BatchNorm aims to reduce this shift by normalizing the inputs of each layer. A BatchNorm layer normalizes the input by subtracting the batch mean and dividing by the batch standard deviation. It then scales and shifts the result using two learnable parameters, gamma and beta.
In the context of CNNs, BatchNorm2D is specifically designed to work with 2D inputs, such as images or feature maps [6]. When applied to a Conv2D layer in a CNN, BatchNorm2D normalizes each feature map independently. This means that for an input with shape (batch-size, channels, height, width), BatchNorm2D will compute and apply the mean and variance for each channel across the batch, height, and width dimensions. The use of BatchNorm2D in CNNs offers several advantages: it allows higher learning rates, potentially accelerating the training process; it reduces the dependency on careful initialization of the network weights; and it acts as a regularizer, in some cases eliminating the need for Dropout [7].
During inference, BatchNorm2D uses a moving average of the mean and variance computed during training, ensuring consistent normalization even when processing single images. While BatchNorm has become a standard component in many CNN architectures, it’s worth noting that alternatives like Layer Normalization or Group Normalization have been proposed for specific use cases or to address certain limitations of BatchNorm [8]. These variations on the normalization theme continue to be an active area of research in deep learning, as practitioners seek to optimize network performance across a wide range of applications and architectures.
Max Pooling.
Max pooling is a downsampling technique commonly used in CNNs to reduce the spatial dimensions of the feature maps while retaining the most important information [9] . The primary purpose of max pooling is to achieve spatial invariance to small translations in the input, reduce computational complexity, and control overfitting. In a max pooling operation, the input feature map is divided into non-overlapping rectangular regions, and for each such region, the maximum value is output to the next layer. This process effectively reduces the resolution of the feature map while preserving the most prominent features detected by the previous convolutional layers.
The most common form of max pooling used in CNNs is 2D max pooling, which operates on 2D feature maps produced by convolutional layers [10]. A typical 2D max pooling layer is characterized by its pool size (usually 2×2) and stride (often equal to the pool size for non-overlapping pooling). For example, a 2×2 max pooling with a stride of 2 will reduce both the height and width of the input feature map by half. This reduction in spatial dimensions leads to a decrease in the number of parameters in the subsequent layers, which helps in controlling overfitting and reduces the computational cost of the network. Additionally, max pooling introduces a form of translational invariance, making the network more robust to small spatial shifts in the input [11].
While max pooling has been widely adopted in many successful CNN architectures, it’s worth noting that alternative pooling methods exist, such as average pooling or strided convolutions. Some recent architectures have even experimented with removing pooling layers altogether, relying instead on increased stride in convolutional layers to achieve downsampling [12]. However, max pooling remains a popular choice due to its simplicity, effectiveness, and biological plausibility, as it mimics certain aspects of the human visual cortex. As CNNs continue to evolve, the role and implementation of pooling layers remain active areas of research in the deep learning community.
METHODS.
In this study, a CNN was utilized for object detection and classification of different 3D shapes from a dataset. The dataset used in this study is the “shapes3d” dataset from Google DeepMind [17, 18], which contains 480,000 labeled images of four different shapes: cube, sphere, cylinder, and ellipsoid. Each image represents a 3D shape from different perspectives, providing a comprehensive set of examples for training a deep learning model. The goal was to develop a model that could predict and categorize these shapes accurately based on the input images. The dataset was split randomly into two parts: 80% for training and 20% for testing. The 80% training set was used to teach the model to recognize and differentiate between the shapes, while the 20% test set was used to evaluate the model’s performance and its ability to generalize to unseen data.
The baseline architecture of the CNN consisted of multiple convolutional layers, each followed by ReLU activation functions and pooling layers. To improve the model’s performance and explore its robustness, I made several modifications to the original architecture. Firstly, I experimented with the number of layers by adding more fully connected (linear) layers and removing some Batch Normalization (BatchNorm2D) layers. The objective was to understand how deeper architectures and the removal of certain normalization techniques affect the learning dynamics and generalization of the model.
I also experimented with varying kernel sizes in the convolutional layers. The goal was to identify the optimal kernel size that would capture the most relevant features of the 3D shapes while balancing computational efficiency. Different kernel sizes, ranging from smaller (2×2) to larger (6×6), were tested to observe their impact on model accuracy. Moreover, I adjusted the dropout levels within the network to prevent overfitting and improve generalization. By increasing and decreasing dropout rates at various layers, I assessed their influence on the overall classification accuracy.
The results of these modifications were evaluated based on classification accuracy. By systematically altering these parameters—such as the number of layers, kernel sizes, and dropout rates—I was able to identify a configuration that provided the optimal balance between model complexity and performance. The findings demonstrated that specific combinations of these parameters significantly enhanced the model’s accuracy, providing insights into the optimal design choices for CNN architectures applied to 3D object classification tasks.
RESULTS.
The experiments conducted to optimize the CNN architecture for 3D shape classification revealed significant insights into the impact of different architectural changes on model performance.
The first experiment focused on understanding the impact of the different layers, as summarized in Table 1. The nomenclature is x (y) where x represents the number of classification layers, while y signifies the number of required dropout and linear layers. The removal of the Batch Normalization (BatchNorm2D) layer had a substantial negative impact on the model’s performance. Without BatchNorm, the model struggled to learn effectively and tended to make random guesses for categorization, leading to an accuracy of about 25 percent. This suggests that Batch Normalization plays a critical role in stabilizing the learning process and ensuring better convergence. Furthermore, adding more linear layers to the network also led to a reduction in accuracy, likely due to overfitting or vanishing gradient problems associated with deeper architectures. However, keeping ReLU activation functions in the network was essential for achieving near-perfect accuracy, as they helped maintain non-linearity and avoid issues like vanishing gradients.
| Table 1. Effect of different layers on accuracy. | ||
| Layers | Accuracy | Notes |
| 3 (3) | 99.61% | conv2d, batchnorm2d, maxpool2d, (dropout, linear, linear) |
| 3 (2) | 99.80% | conv2d, batchnorm2d, maxpool2d, (dropout, linear) |
| 2 (2) | 25.03% | conv2d, maxpool2d, (dropout, linear) |
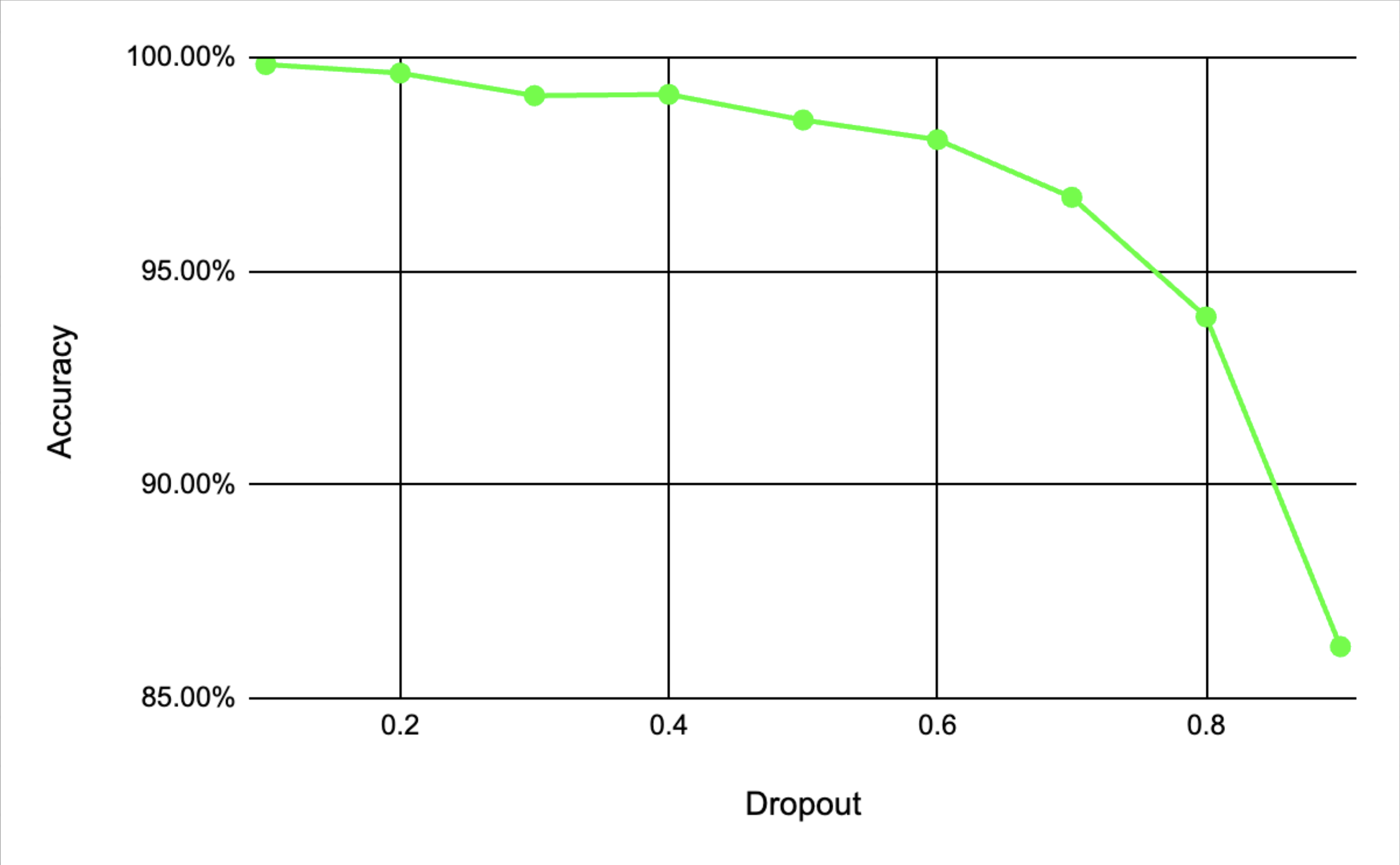
The effect of varying dropout rates on model accuracy was also tested. Gradually increasing the dropout rate beyond a certain threshold caused the model’s accuracy to decline (Figure 2). This is likely because higher dropout rates lead to excessive regularization, which prevents the model from learning important patterns in the data. Among the values tried, the best dropout rate was found to be 0.1, where the model maintained a balance between preventing overfitting and retaining sufficient feature learning, resulting in the highest accuracy.
Finally, the effect of kernel size in the convolutional layers was examined. It was observed that a kernel size of 5 produced the most accurate results for the model (Figure 3). Initially increasing the kernel size improved the model accuracy as the kernel was able to capture the context. When the kernel size was increased to 6 or more though, the model’s accuracy began to drop marginally. This drop in performance could be attributed to larger kernels capturing more irrelevant information or noise, thereby reducing the model’s ability to focus on the most salient features of the 3D shapes.

These results demonstrate the importance of carefully tuning the architecture and hyperparameters of CNNs for optimal performance in object detection and classification tasks. Parameters such as dropout rates, kernel sizes, and the inclusion of normalization layers are crucial in determining the model’s ability to generalize well to unseen data.
CONCLUSION.
This study explored the use of CNNs for object detection and classification of 3D shapes, focusing on how various architectural modifications and hyperparameter adjustments affect model performance. The results demonstrated that careful tuning of parameters such as dropout rates, kernel sizes, and the inclusion of Batch Normalization layers significantly impacts the accuracy of the model. An optimal dropout rate of 0.1 was identified, as higher rates led to over-regularization and reduced accuracy. Similarly, a kernel size of 5 was found to be the most effective, while larger kernels caused a decline in performance due to the model capturing irrelevant features. The removal of Batch Normalization layers resulted in drastic accuracy drops, highlighting their importance in stabilizing learning and improving convergence.
These findings underscore the need for a balanced and methodical approach when designing CNN architectures for 3D object classification tasks. Future work could involve exploring advanced techniques such as transfer learning, more complex architectures like Residual Networks (ResNets), or employing other regularization methods to further enhance performance. Overall, this research contributes valuable insights into the optimal design and parameter choices for CNN-based 3D shape classification, paving the way for more efficient and accurate models in similar applications.
ACKNOWLEDGMENTS.
I am thankful to Joshua Fernandez (Georgia Institute of Technology) for his valuable guidance and mentorship.
REFERENCES
1 B. Kim, Y. Natarajan, S. D. Munisamy, A. Rajendran, K. R. Sri Preethaa, D. E. Lee, G. Wadhwa, Deep learning activation layer-based wall quality recognition using Conv2D ResNet exponential transfer learning model. Mathematics 10, 4602 (2022).
2 S. Kundu, S. Prakash, H. Akrami, P. A. Beerel, K. M. Chugg, psconv: A pre-defined sparse kernel-based convolution for deep cnns. In 2019 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), IEEE, pp. 100-107 (2019).
3 Z.-Q. Cheng, Q. Dai, H. Li, J. Song, X. Wu, A. G. Hauptmann, Rethinking spatial invariance of convolutional networks for object counting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 19638-19648 (2022).
4 S. Sophia, et al., Human behaviour and abnormality detection using yolo and conv2d net. In 2024 International Conference on Inventive Computation Technologies (ICICT), IEEE, pp. 70-75 (2024).
5 S. Ioffe, Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167 (2015).
6 Y. Wu, K. He, Group normalization. In Proceedings of the European Conference on Computer Vision (ECCV), pp. 3-19 (2018).
7 S. Santurkar, D. Tsipras, A. Ilyas, A. Madry, How does batch normalization help optimization? Advances in Neural Information Processing Systems 31 (2018).
8 J. Ba, Layer normalization. arXiv preprint arXiv:1607.06450 (2016).
9 D. Scherer, A. Müller, S. Behnke, Evaluation of pooling operations in convolutional architectures for object recognition. In International Conference on Artificial Neural Networks, Springer, pp. 92-101 (2010).
10 A. Krizhevsky, I. Sutskever, G. E. Hinton, Imagenet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems 25 (2012).
11 I. Goodfellow, Deep Learning, MIT Press (2016).
12 J. T. Springenberg, A. Dosovitskiy, T. Brox, M. Riedmiller, Striving for simplicity: The all convolutional net. arXiv preprint arXiv:1412.6806 (2014).
13 K. Simonyan, Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556 (2014).
14 K. He, X. Zhang, S. Ren, J. Sun, Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 770-778 (2016).
15 J. Redmon, S. Divvala, R. Girshick, A. Farhadi, You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 779-788 (2016).
16 K. He, G. Gkioxari, P. Dollár, R. Girshick, Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, pp. 2961-2969 (2017).
17 C. Burgess, H. Kim, 3d shapes dataset. https://github.com/deepmind/3dshapes-dataset/ (2018).
18 C. Burgess, H. Kim, 3d shapes dataset. https://tensorflow.org/datasets/catalog/shapes3d/ (2018).
Posted by buchanle on Wednesday, June 25, 2025 in May 2025.
Tags: Computer Vision, Machine learning, Model Optimization, Neural Networks, Object Detection

