The Angle of the Cable of a Cable-Stayed Bridge VS the Maximum Load Carried by the Bridge
ABSTRACT
Bridges are structures that have been built since the stone age.[1] Nowadays, they play an essential role in the world of fast transportation and trade, in which engineers are trying to find solutions to create longer and stronger bridges through different perspectives – materially, structurally, and physically. In this work, I hypothesized that as the angle of the cables (from the mast to the cable) of a harp-shaped cable-stayed bridge increases, it decreases its maximum load that it can carry. I recorded the maximum carried load at an angle of 63.44˚ to be 16.36 N; as the angle decreased, the maximum load increased, reaching 28.02 N at an angle of 21.17˚. However, there is an unexpected outcome shown in the data: the increase rate of the maximum load plateaued as the angle further decreased, only reaching to 28.32 g at an angle of 13.17˚; the maximum tension even decreased to only 26 N at 5.42˚.
INTRODUCTION.
In the early days, bridges were usually built by stone or wood due to their characteristics of being secure under high pressure but vulnerable under tension, they were usually built in the form of arches and were short in length. Their appearance would not change until the industrial revolution, when factories started to mass manufacture.[2] These materials can experience more tensile strength, causing them to withstand load for a longer distance, influencing them to become longer and exhibit increasingly unique designs.[3]
Bridges are getting longer to compensate for the long journeys, trying to make travelers more convenient. The construction of the Hong Kong-Zhuhai-Macau Bridge, the longest open-sea fixed link in the world that includes three cable-stayed bridges, finished in 2018,[4] it challenged many engineers throughout the world to use physics to open new horizons; to build bridges that can withstand the maximum load and can send people on their longest adventures.
Nowadays, there are many types of bridges: suspension bridge, truss bridge, and beam bridge just to name a few. One of the most used types of bridges is the cable-stayed bridge. Cable-stayed bridges have one or more towers, with several cables connecting the mast to the horizontal beam. They can be classified into 4 different types: harp design with all the cables lined up parallelly, radial design with all the cables attached to one point on the mast, star-shaped design with cables connected to two opposite points of the pier, and fan design being a combination of the harp and radial design.[5] They can look similar to suspension bridges – both using the tension in the cables to compensate for the load. However, the main difference is that while suspension bridges can be built in longer distances, they are able to carry less load than cable-stayed bridges.
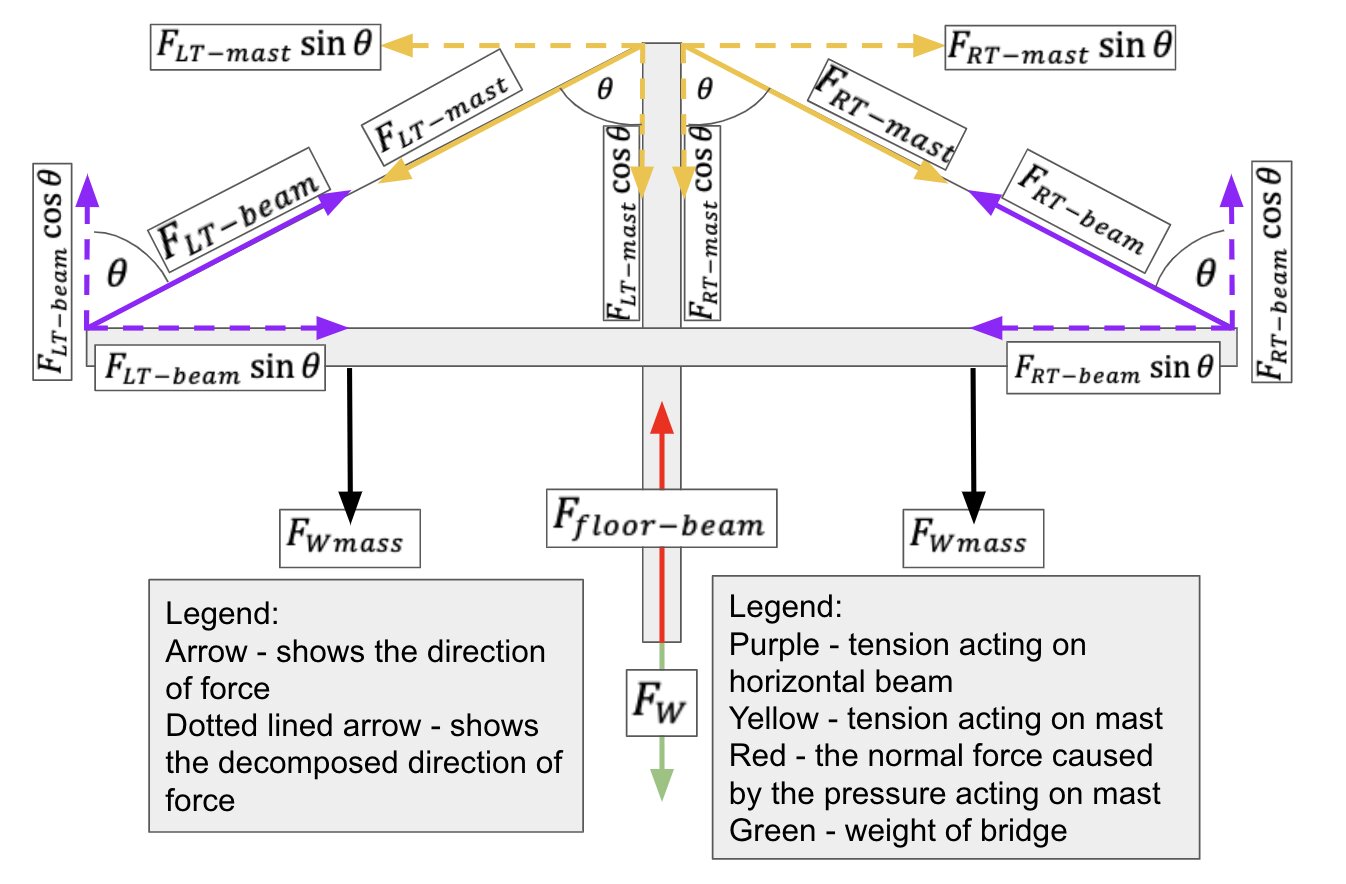
In this research, I will be focusing on cable-stayed bridges. The physics behind can be explained using trigonometry and Newton’s Laws of Motion. In the diagram, we assume that the tensile forces on the threads of both sides are equal, it is stationary and is at its equilibrium state.
According to Newton’s third law, when the thread exerts a tensile force measured in Newtons on the horizontal beam, that the horizontal beam would exert a force that is equal in magnitude and opposite in direction on the thread,[6] hence pulling the mast shown in the diagram above. Using trigonometry functions and Pythagoras theorem, both tensile forces can be derived into their vertical and horizontal components.[7] Therefore, we can use equation 1 below to explain the Newton’s third law experienced in the tensile forces of the thread:
\[F_{LT-mast}=F_{LT-beam}\tag{Eq. 1}\]
and
\[F_{RT-mast}=F_{RT-beam}\tag{Eq. 2}\]
where is the left tensile force acting on the mast (shown in yellow in figure 1), is the left tensile force acting on the beam (shown in purple in figure 1), is the right tensile force acting on the mast (shown in yellow in figure 1), and is the right tensile force acting on the beam (shown in purple in figure 1).
Figure 1. Free body diagram showing the forces and the decomposed vectors of a cable-stayed bridge with 1 cable
Both vertical tensile forces components are separated from the original tensile force vector by an angle of θ, by using Newton’s third law, they add up with the downward weight of bridge and exert a force of pressure on the top of the mast downwards, causing the floor to also exert a force same in magnitude but opposite in direction towards the mast. According to Newton’s first law, it will remain in equilibrium since there are no resultant forces acting on the mast,[8] which can be represented in the following equation:
\[{(F}_{LT-mast}+F_{RT-mast})\cos{\theta}+F_W=F_{floor-beam}\tag{Eq. 3}\]
where is the weight of the bridge, is the force applied from the floor acting on the beam, and is the angle between the main vector and the decomposed vertical vector component.
Focusing on the two horizontal components of tension acting on the mast bridge. Due to the magnitudes of them being equal but opposite in direction, it has no resultant forces. Thus, according to Newton’s first law, it will remain in equilibrium.
\[F_{LT-mast}\sin{\theta}-F_{RT-mast}\sin{\theta}=0\tag{Eq. 4}\]
On the horizontal beam of the bridge, there are two horizontal components of tension of equal magnitude but opposite direction acting on it. This causes no resultant forces and hence it will remain in equilibrium.
\[F_{LT-beam}\sin{\theta}-F_{RT-beam}\sin{\theta}=0\tag{Eq. 5}\]
Finally, the vertical component of the tension acting on the horizontal beam will compensate for the downward weight generated by the load. These two forces are equal if the horizontal beam is not moving, thus no resultant forces. Therefore, according to Newton’s first law, it will remain in equilibrium.
\[F_{LT-beam}\cos{\theta}+F_{RT-beam}\cos{\theta}=F_{Wmass}\tag{Eq. 6}\]
where is the weight of the masses combined.
The bridge will collapse when the downward weight of the load surpasses the maximum tensile force that was held by the thread on the horizontal beam available in a vertical component.
MATERIALS AND METHODS.
This experiment is carried out partially in the school laboratory and partially at home, therefore the materials I have chosen are low-cost and easy to find. Due to sustainability reasons, I have used old cardboard boxes for the structure of the bridge model instead of using wood.
Assembly of the mast of the bridge.
The length of the mast of the bridge does not affect the final results. Before the assembly of the mast, I have selected a few cardboard boxes that are in good quality (stiff and undamaged), have chosen to cut 6 pieces of cardboard in the area dimensions of 200cm x 10cm. When sticking the pieces together, the folds must be attached with them facing each other to avoid a buckling effect. Extra tape is used to further reinforce the mast by taping around the mast at the bottom and around the folds.
I placed in total 4 eye-hook screws both front and back of the mast, with the same separation on both sides. To reinforce the screws, I simply applied UHU glue around the tip, thread, and shank of the eye-hook screw. If the screws start to deform from its original position, I translated the 4 eye-hook screws to another position on the mast, keeping a constant separation.
To make the mast stand up easily, a sturdy platform is made to support it. The size and style of the platform does not interfere the final results.
Assembly of the beam of the bridge.
The beam of the bridge is also made from cardboard. I cut out 6 pieces of rectangular cardboard with area dimensions of 100cm x 10cm with a hole in the center of 12cm x 7cm. Then, I stacked them up and attached them together with the method similar to the mast. Use some tape to tape around the borders of the beam and around the hole in the beam without creases since it acts as a string-like material that is applying tensile strength onto the beam to avoid bending.
On the left side of the hole, starting from 3 cm into the beam from the width, and 2 cm from each side of the length, place 2 eye hook screws, and repeat this step with 6 cm intervals until it reaches the hole. It is then repeated again to complete the other side of the hole in the beam. In total, the beam should have 28 eye hook screws. UHU glue is applied around the tip, thread, and shank of the eye-hook screw to further reinforce them.
Finally, measure the weight of the beam. This value will be added to the results when carrying the experiment.
Method of Carrying out the Experiment.
Place the mast through the hole of the beam. Four pieces of thread, with 2 markings of a separation 45cm drawn on each thread, is cut way beyond the markings. The ends of the thread is tied on to the outer-most screws of the beam and the corresponding screw on the mast using a round-turn-two-half-hitches knot at the marking. Place the finished bridge section into the platform. Additional reinforcement can be further added by using two pieces of big items (e.g. furniture) to clamp the bridge.
Place the masses (100g) two by two (one on each side) quickly on to the beam. When it reached towards its range of breaking, switch to 10g and 50g masses to achieve precise data. When placing the masses, try to even out where they are placed so that the pressure on the whole beam is even, and torque and slanting is avoided.
Since the thread is a natural material and will elongate with weight as time passes by, the masses must be placed quickly so that there is minimum error in the data.
Table 1. Results recorded from the experiment investigating how the angle between the mast and thread affect the maximum load
| Data Set No. | The Angle between mast and thread (˚) | Maximum Load (N) | |||||
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | Avg. | ||
| 1 | 63.44 | 17.66 | 16.09 | 18.05 | 16.28 | 13.73 | 16.36 |
| 2 | 49.56 | 18.64 | 18.87 | 20.80 | 18.25 | 18.05 | 18.52 |
| 3 | 38.89 | 20.60 | 18.05 | 20.80 | 24.53 | 19.62 | 20.72 |
| 4 | 29.63 | 23.54 | 25.51 | 21.58 | 23.94 | 22.76 | 23.47 |
| 5 | 21.17 | 29.43 | 30.61 | 23.54 | 29.04 | 27.47 | 28.02 |
| 6 | 13.17 | 28.45 | 28.65 | 28.45 | 28.45 | 27.66 | 28.33 |
| 7 | 5.42 | 26.49 | 25.51 | 26.09 | 18.05 | 13.73 | 26 |
*Trials 4 and 5 of data set 7 (in red) were eliminated due to anomalies.
RESULTS.
Analysis of data.
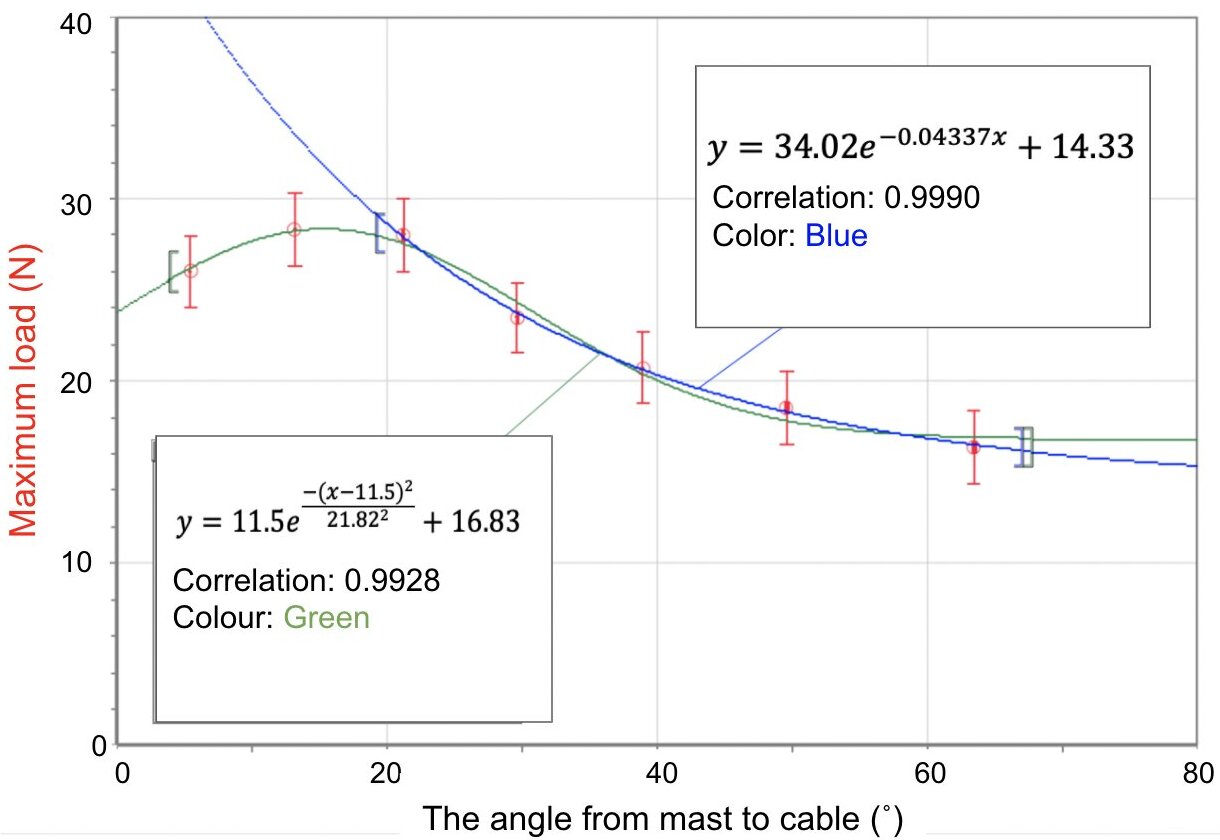
As the angle between the mast and the string increases, using equation (6), it shows that the value of both vertical components of the tensile forces acting on the beam of the bridge decreases. The graph records the most maximum load of 28.02 N at an angle of 21.17˚. As the angle increased to 63.44˚, the maximum load decreased, reaching 16.36 N. A line of best fit is plotted against the results, which shows that the maximum load of the bridge that it can carry decreases exponentially.
Nevertheless, the values for data 6 and 7 (13.17˚ and 5.42˚ respectively) were out of my range of prediction; in which the values for data set 7 were even below data set 6. The data sets were then plotted against the other data sets with a line of best fit; the maximum load increased as the angle decreased, but after 13.17˚, the maximum load decreased as well. This was not as predicted in my hypothesis.
After finding out this anomaly, I tested the “stretchiness” of the string by hooking the string onto different masses of different weights and measuring the extension. Hooke’s law states that if a material obeys the law, it must have a directly proportional unit tensile force to unit length in the extension.[9] By applying to Hooke’s law equation, I can also find out the spring constant of the string:
\[F_T=-kx\tag{Eq. 7}\]
where is the tensile force of the string and is the extension of the string under stretching.
Since in this investigation, the weight is equal to the tensile force due to Newton’s third law, therefore we can use the following expression:
\[F_{W-mass}=-kx\tag{Eq. 8}\]
where is the weight of the mass put on the thread.
When I tested out the string using Hooke’s Law, I made sure that the masses are put as quick as possible, since long-term stretching can cause deformation to the string. The results yielded in a pattern that it started off every unit of weight added is directly proportional to its extension. Nevertheless, after a certain point, the string was much easier to stretch and lead towards a breakage. This shows that the material, after a certain point of tension, does not obey Hooke’s law.
As the angle of the string between the mast decreases, there will be an increase in the ratio of the vertical tension component acting on the horizontal beam in comparison to the corresponding horizontal component. This causes the Hooke’s law effect to be amplified. Hence, it caused the thread to break earlier than predicted.
DISCUSSION.
Relating back to hypothesis.
My hypothesis stated that as the angle from the mast to the cable of a harp-shaped cable-stayed bridge increases, it decreases its maximum load that it can carry. After the experimental and data analysis process, it has proven my hypothesis to be partially correct. From 21.17˚ to 63.44˚, the results have shown that the maximum load increased as the angle decreased. However, if the cable of the bridge was set up at a smaller angle, the results yielded differently; instead of continuing to increase, it had a lower maximum carried load than expected.
Optimal angle.
To calculate the optimal angle, I simply differentiated the Gaussian equation shown in figure 2 in green.
Figure 2. Graph showing the values (data set 1 – 5) that follow my hypothesis (line of best fit shown in blue), and those that do not follow the prediction made in the hypothesis due to Hooke’s Law (line of best fit shown in green)
\[y=11.5e^\frac{{-(x-11.5)}^2}{{21.82}^2}+16.83\tag{Eq. 9}\]
\[\frac{dy}{dx}=-\frac{(57500x-881475)e^{-\frac{2500{(x-15.33)}^2}{1190281}}\tag{Eq. 10}\]
where is the maximum load and is the angle of the cable to mast.
Since I am finding the optimal angle, hence I will need to let the differential equation (8) to be 0 to find the turning points.
\[0=-\frac{(57500x-881475)e^{-\frac{2500{(x-15.33)}^2}{1190281}}}{1190281}\tag{Eq. 11}\]
\[x=15.33\tag{Eq. 12}\]
Therefore, it shows that the bridge will carry the most load at 15.33˚.
Errors and improvements.
The main error presented in this project is that I did not account for the point that the thread starts to become a non-Hookian material. Although this did not cause any effect towards the majority of the results, it seriously affected the results of data set 6 and 7 (13.17˚ and 5.42˚ respectively) where they involve in smaller angles between the cable and the mast. I initially chose thread as my material since it is low-cost and easier to break. To improve the experiment, I could have used an artificial fiber that obeys Hooke’s law for a larger force, but at the same time is easy to break.
Limitations.
It is stated in the methodology section that the masses are put evenly across the beam to even out pressure and avoid the beam undergoing slanting or torque. However, this is impossible due to human error that a very slight slanting of the beam can be seen when carrying out the experiment.
The unpredictable outcome.
Although the anomaly caused unreliable data for the smaller angles, it mimics the effect and explains why all harp-shaped cable-stayed bridges in real life do not have very small angles between the cables and the mast. When engineering, a safety margin is necessary to ensure that the structure is safe at all situations, therefore redundancies, such as having several cables holding the beam and having a bigger angle between the cable and the mast, is made into the designs of the bridge. For example, there is an investigation on the cable optimization of the long-span cable-stayed bridge in La Coruña which investigates on the distribution, number, and angle of cables.[10]
Extensions.
An extension towards investigating which types of bridges are the most beneficial towards which types of locations can be done to further understand the implications of a structural engineers decision process. Also, the effect of the wind causing torsional dynamics and angular acceleration can cause drastic effect to a bridge, thus can be investigated.[11]
ACKNOWLEDGMENTS.
I would like to acknowledge Ms. Gemma Mackintosh, my physics teacher, for supporting me throughout the experimental process.
REFERENCES.
- MERDINGER, C. J. (1961). Bridges through the Ages: Part 1. The Beginning. 53(353). Retrieved from https://www.jstor.org/stable/44568788?seq=1#metadata_info_tab_contents
- Steel made the industrial revolution a reality. (n.d.). Retrieved from https://www.jsw.in/steel/how-iron-and-steel-fuelled-industrial-revolution
- Steel Production. (n.d.). Retrieved from https://courses.lumenlearning.com/suny-hccc-worldhistory2/chapter/steel-production/
- Hong Kong – Zhuhai – Macao Bridge (HZMB) Hong Kong Section. (n.d.). Retrieved from https://www.hzmb.gov.hk/en/
- Thaler, D. (2020). Analysis & Design of Cable Stayed Bridge. Retrieved from https://www.infrastructurepc.com/analysis-design-of-cable-stayed-bridge/
- Newton’s Laws of Motion. (n.d.). Retrieved from https://www1.grc.nasa.gov/beginners-guide-to-aeronautics/newtons-laws-of-motion/
- Marghitu, D. B. (2001). Force Vector. Retrieved from https://www.sciencedirect.com/topics/engineering/force-vector
- Tsokos, K. A. (2014). Physics for the IB Diploma. Cambridge University Press.
- Williams, M. (2015). What is Hooke’s Law? Retrieved from https://phys.org/news/2015-02-law.html
- Baldomir, A., Hernandez, S., Nieto, F., & Jurado, J. A. (2010). Cable optimization of a long span cable stayed bridge in La Coruña (Spain).
- Wilson, J. C., & Gravelle, W. (1991). Modelling of a cable-stayed bridge for dynamic analysis.
Posted by John Lee on Saturday, May 7, 2022 in May 2022.
Tags: Bridges, Engineering, Forces, Hooke’s Law, Physics