Radiation Emissions of Primordial Black Holes as Dark Matter in a Dwarf Galaxy
ABSTRACT
It is believed dark matter (DM) comprises 84% of all matter in the universe though it is not directly observable, and its composition remains unclear. Current cosmological models show primordial black holes (PBHs), black holes formed during the inflationary period right after the Big Bang, may constitute a large majority of dark matter. PBHs may convincingly mimic the behavior of DM, not interacting with light while exerting detectable gravitational effects on nearby bodies. This project treated all dark matter particles in an N-body simulated dwarf galaxy as PBHs. Each “black hole” was allowed to accrete gas and emit light as the in falling gas was converted to energy, and the accretion rate, luminosity, and magnitude of each primordial black hole was calculated. These data indicated that most PBHs would produce no detectable light, consistent with current knowledge of DM, but few very luminous black holes could be detectable, possibly in the X-ray spectrum as bright sources, providing a possible explanation for observations of X-ray bursts.
INTRODUCTION.
Current understanding regarding the composition of the Universe indicates that the majority of the Universe (about 30% of total mass energy, 84% of all matter) is composed of dark matter (DM) [1].
While baryonic (ordinary) matter can be observed interacting with gravitational and electromagnetic forces, dark matter only interacts with gravitational forces- that is, dark matter cannot be seen in the literal sense as it does not emit, absorb, or reflect light, but its existence can be inferred by the gravitational effects it exerts on baryonic, observable matter [1]. For instance, if a galaxy is analyzed for its total baryonic matter content, it will become apparent that the amount of observable matter present is much less than the amount of matter required for the galaxy to hold itself together [1-3]. Furthermore, computer models of the Universe that contain only visible matter do not resemble observations of the Universe. It is only when the correct amount of a non-visible but gravitationally active dark matter is accounted for in these simulations that the macro structure of simulated Universes begin to resemble that of the actual Universe [1,3].
Due to its importance and prevalence in the Universe, a great effort has been made to understand dark matter by trying to detect it, and these efforts can be separated into two main branches. One branch, direct detection, tries to detect particles such as neutrinos and weakly interacting massive particles as they interact with normal matter [4]. These processes typically utilize underground caverns filled with mineral oils and lined with photodetectors to detect the results of dark matter-baryonic matter interactions in the form of photons [5]. The other branch, indirect detection, deals with trying to detect dark matter-dark matter interactions which result in observable emissions (such as gamma rays) in outer space [6]. Efforts to detect dark matter as energy missing from proton beam collisions in the Large Hadron Collider also are included under the umbrella of indirect detection [4,7].
Despite intense international efforts, the composition of dark matter is still not understood. One proposal is that dark matter may be composed of primordial black holes (PBHs), black holes which formed in the early Universe [8]. These black holes would have formed in the inflationary period during which space-time of the early Universe is thought to have explosively expanded in a very short time. This PBHs as dark matter hypothesis has often been discredited, however, as it dictated that the primordial black holes involved must be very small, and black holes of that size would most assuredly have evaporated by our present time [9,10]. Other criticisms include that the evaporation of PBHs in the early Universe would have caused significant distortions to the cosmic microwave background (CMB), distortions not seen in observations today [9,10]. However, Clesse and García-Bellido proposed a model of dark matter as being entirely composed of PBHs and gave an estimated mass range of 10-20 M☉ ≲ MPBHs ≲ 105 M☉ that these black holes must fall within in order to not have evaporated away by this present epoch [11]. In addition, this paper proposed a model in which the merger of smaller PBHs resulted in massive black holes, possibly forming the supermassive black holes present in the centers of galaxies today, without distorting the CMB [11]. This current study assumed that the model of dark matter as PBHs as outlined in this 2015 paper was correct and quantified the radiation from PBHs expected of such a model.
METHODS.
We simulated a dwarf galaxy using the N-body process which represents a system of masses with point sources of mass. The motions of these mass particles due to forces resulting from their interactions were approximated. Models of relativity and hydrodynamics governed the interactions of these particles in order to produce a situation in which the behavior of these particles models the behavior of their real life counterparts as closely as possible [3].
The next step was to locate each particle of dark matter and then to replace each dark matter particle with a black hole of equivalent mass. Then, the average gas density around each black hole was calculated along with the speed of the black hole relative to the surrounding gas. These metrics were then utilized to calculate the Bondi accretion rate (an approximation of the amount of mass a spherically accreting black hole accretes per unit of time) of these black holes using the following formula:
\[{\Delta M}_{BH}=\frac{4\pi G^2{M^2}_{BH}\rho}{{{{(c}^2}_{gas}+{v^2}_{BH})}^\frac{3}{2}}\]
Where:
- ΔMBH is the accretion rate of the black hole in solar masses per million years (M☉/myr).
- G is the universal gravitational constant in pcM☉-1(km/s)2.
- MBH is the mass of a black hole in solar masses (M☉).
- ⍴ is gas density around a black hole in solar masses per cubic parsec (M☉/pc3).
- C is the gas speed in kilometers per second (km/s).
- VBH is the relative speed of the black hole to the gas around it in kilometers per second (km/s).
All black holes were assumed to accrete all matter within a 0.1 parsec radius, (0.1 parsec was the minimum resolution of the simulation. Actual accretion radii of black holes is less than 0.1 pc) and it was assumed that each black hole would convert accreted matter to energy at a 4% efficiency as is the standard assumption based off of accretion disk models [12].
Luminosities were calculated from the total energy released by each black hole. These luminosities were then converted into total apparent magnitudes. These two measures of brightness were used evaluate the feasibility of the PBHs as DM hypothesis.
Observations indicate that most of the Universe is not saturated with bright X-ray sources [13]. However, hotspots and burst sources of X-ray emission have been detected. If the PBHs as DM hypothesis is to be supported, most or all black holes in the simulation should have relatively low amounts of radiation emission. Some black holes may be extremely bright, and those may be possible contributors to X-ray burst sources. These extremely bright black holes should, however, be in the minority of all black holes.
RESULTS.
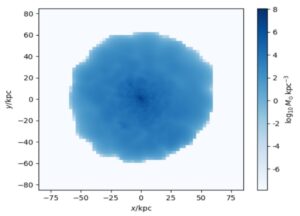
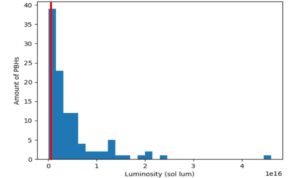
The black holes were distributed in a wide halo around the center of the dwarf galaxy with a density distribution exactly matching that of the dark matter particles which they replaced. An intensely dense region of dark matter is seen in the nucleus of the galaxy and a more diffuse spiral distribution is seen throughout the rest of the galaxy (Figure 1). Most black holes in this simulation were found to be exceedingly dim due to the great distance between the black holes and the point from which they were “observed” (Figure 2). The average luminosity of the black holes was 2×1013 solar luminosities, indicating that they release 20 trillion times more energy than the sun. This energy is primarily expected to be emitted in the X-ray spectrum [14] and thus not directly observable at visible wavelengths. The average apparent magnitude of the black holes was 100. These findings are consistent with observations of cosmic background radiation in the X-ray spectrum [13] in which most of the Universe is not saturated with an overabundance of bright X-ray sources.
Figure 1. The black hole distribution within the dwarf galaxy is shown. A high density of black holes is located at the center of the galaxy and a lower density is located at the edges.
Figure 2. The luminosities of all black holes are displayed as a histogram. The red line marks the mean luminosity of 2×1013 solar luminosities. Most black holes have very low luminosities while one group has a significantly higher luminosity of ~4.5×1016 solar luminosities.
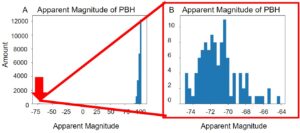
However, a small portion of black holes were found to be extraordinarily bright with apparent magnitudes of -60 and below (Figure 3). There were 108 black holes found to be at or below a magnitude of -60, and they could be a source of observed X-ray bursts if PBHs indeed compose a majority of dark matter [14].
Figure 3. (a) The apparent magnitude of all black holes and (b) a zoomed in view of the small portion of black holes with exceedingly low magnitudes (at location of red arrow) are shown. Most black holes are exceedingly dim (high apparent magnitude means low brightness); however, those found at the location of the red arrow demonstrate exceptionally high brightness. These particular PBHs may be sources of X-ray bursts.
SUMMARY AND FUTURE DIRECTIONS.
In this work, dark matter in a simulated dwarf galaxy was treated as black holes and the theoretical amount of radiation that would be emitted by each of those black holes was calculated. The data indicated that if primordial black holes did indeed constitute dark matter, the radiation signatures of these black holes could be consistent with observational data of the cosmic X-ray background [13].
To our knowledge, this study was one of the first attempts in analyzing the radiation signatures of primordial black holes as dark matter in a simulation. However, this simulation was lacking in its resolution, resulting in an intrinsically inaccurate representation of black hole accretion radii. Actual accretion of black holes is still a highly debated topic with no clear consensus the physics involved such as the importance of turbulence or magnetic fields. We adopted a standard thin-disk accretion model with an accreted mass to energy conversion efficiency of 4% as given by Shakura and Sunyaev [12], but this figure would change depending on the black hole spin and accretion model. The typical accretion scale of a black hole would be more than 100 times smaller than the 0.1 kpc radius used (minimum resolution of the simulation), so this simulation is unable to resolve the physics of accretion.
This study also did not evaluate the impact of PBHs on cosmic evolution, including how black hole mergers could affect macrostructure. It is suggested that future studies of PBHs as dark matter analyze how the formation of stars, galaxies, and large scale structure of the Universe would be affected if a simulation was run with PBHs replacing dark matter as a starting parameter as opposed to our approach of treating dark matter as PBHs for post simulation analysis. It is understood that to achieve the necessary resolution and time scale within such a simulation would be exceedingly computationally expensive; however, it would provide unequivocal insight into the PBHs as dark matter hypothesis.
ACKNOWLEDGMENTS.
We would like to express gratitude to Dr. Kelly Holley-Bockelmann of the Vanderbilt Department of Physics and Astronomy for allowing us to work in her astronomy group as well as providing guidance throughout this project as a mentor. We would like to thank Dr. Ferah Munshi also of the Department of Physics and Astronomy for providing the simulation used in this project. We thank John Hood and the other graduate students in the Department of Physics and Astronomy for their help with code troubleshooting, and we thank Dr. Lesa Brown and all other at the School for Science and Math at Vanderbilt for their support.
REFERENCES.
- N. Comins, W. Kaufmann III, Discovering the Universe, 8th ed. New York: WH Freeman and Company. 315, 414-416, 447-470 (2008).
- J. Kormendy, L. Ho, Coevolution (Or Not) of Supermassive Black Holes and Host Galaxies. Annual Review of Astronomy and Astrophysics 51, 511-653 (2013).
- R. Somerville, R. Davé, Physical Models of Galaxy Formation in a Cosmological Framework. Annual Review of Astronomy and Astrophysics 53, 51-113 (2015).
- G. Bertone, D. Hooper, J. Silk, Particle dark matter: evidence, candidates and constraints. Physics Reports 405, 279-390 (2005).
- Deep Underground Neutrino Experiment. Neutrino Detectors – Deep Underground Neutrino Experiment. (2017) [online] Available at: http://www.dunescience.org/neutrino-detectors/.
- Fermi.gsfc.nasa.gov. Fermi Gamma-ray Space Telescope: Exploring the Extreme Universe. (2017) [online] Available at: https://fermi.gsfc.nasa.gov/science/eteu/dm/.
- Home.cern. Dark matter | CERN. (2017) [online] Available at: https://home.cern/about/physics/dark-matter.
- B. Carr, S. Hawking, Black Holes in the Early Universe. Monthly Notices of the Royal Astronomical Society 168, 399-415 (1974)
- Y. Ali-Haïmoud, M. Kamionkowski, Cosmic microwave background limits on accreting primordial black holes. Physical Review D 95 (2017).
- S. Clesse, J. García-Bellido, The Clustering of Massive Primordial Black Holes as Dark Matter: Measuring their mass Distribution with Advanced LIGO. Physics of the Dark Universe 15, 142-147 (2017).
- S. Clesse, J. García-Bellido. Massive primordial black holes from hybrid inflation as dark matter and the seeds of galaxies. Physical Review D 92, 1-17 (2015).
- N. Shakura, R. Sunyaev, Black Holes in Binary Systems: Observational Appearances. Symposium – International Astronomical Union 55, 155-164 (1973).
- A. Fabian, X. Barcons, The Origin of the X-Ray Background. Annual Review of Astronomy and Astrophysics 30, 429-456 (1992).
- S. Woosley, Gamma-ray bursts from stellar mass accretion disks around black holes. The Astrophysical Journal 405, 273 (1993).
Posted by John Lee on Thursday, December 24, 2020 in May 2018.
Tags: Cosmological Simulations, dark matter, Primordial Black Holes