Breaking Down the Development of Children’s Ordinality Understanding
ABSTRACT
Children’s early number skills are strong predictors of later mathematical ability and life success. One skill of specific interest is understanding the order that numbers go in, referred to as ordinality. The overall aim of this study is to better understand the development of children’s ordinality knowledge for both number words and written numerals. Children (N = 18) completed four tasks that tested their magnitude and ordinality knowledge for number words and for numerals. Their number word ordinality knowledge was significantly correlated with their numeral ordinality knowledge, and their number word ordinality knowledge was significantly greater than their numeral ordinality knowledge. This study sheds light on the trajectory of children’s ordinality knowledge development and could potentially be used to help tailor methods to improve children’s ordinality knowledge more effectively during formal math instruction.
INTRODUCTION.
Early number skills are important for later academic achievement and life success [1, 2, 3]. Four-year-old children’s numerical reasoning skills are related to their mathematical knowledge at age 15, even after considering other factors such as IQ, reading comprehension, working memory, and familial socioeconomic status (SES) [1]. In addition, early number skills are also related to overall academic performance [2]. Continuing this trend, both early and later math skills also seem to be related to later life outcomes. Seven-year-old children’s math skills are correlated with their SES as adults, beyond the effects of other factors including reading achievement, IQs, and SES of the child’s birth family [3]. High-school math performance specifically has also been found to be related to job quality, salary, and healthcare decisions [4, 5]. Given all these far-reaching implications of early number knowledge, it is important to understand how early number skills develop in children.
One particular skill of recent interest is ordinality knowledge, which deals with our understanding of the order of numbers (e.g., 5 comes after 4, but is before 6). While past research has linked ordinality knowledge to greater arithmetic competence and early school math performance [6], less is known about how ordinality knowledge develops in the first place and what skills may assist in such development. This study focuses on the development of ordinality knowledge for both verbal number words (e.g., “one, two, three…”) and written numerals (e.g., “1, 2, 3…”).
There are several aspects of children’s ordinality knowledge and development that previous research has not fully explored. One aspect of primary focus for this study is the exploration of various number skills that may be associated with children’s numeral ordinality knowledge. Here, the current study targets two magnitude skills (the ability to compare the sizes of number words or numerals) and the number word form of ordinality knowledge. As such, the specific skills analyzed in this study are number word magnitude knowledge (e.g., comparing the sizes of spoken number words like “one” versus “three”), numeral magnitude knowledge (e.g., comparing the sizes of visual numerals like “1” versus “3”), and number word ordinality knowledge (e.g., ordering a series of number words in increasing value). Previous research has found relations between numeral magnitude and numeral ordinality knowledge; specifically, children’s performance on a numeral comparison task (e.g., comparing between digits such as 1 vs. 2) at the end of kindergarten predicted growth in non-adjacent ordering (i.e., ordinality) ability at the end of first grade [7, 8]. However, associations with number word magnitude and number word ordinality are novel explorations from the current study. Such analyses will help further our understanding into what early number skills could aid children in advancing their numeral ordinality knowledge. One specific focus of the study is how children’s spoken number word ordinality knowledge may relate to their written numeral ordinality knowledge. Young children often gain familiarity with number words first from being introduced to numbers orally by a parent or teacher. With recent research suggesting that children may use an existing symbol they know (ex. a heard number word) to learn a new symbol (ex. a corresponding visual numeral) by associating the two, it is possible that children’s knowledge of number words (e.g., “one, two, three…”) helps them develop knowledge of written numerals (e.g., 1, 2, 3…) [9]. Thus, it is important to verify this connection between number words and numerals. Overall, the results in this study shed light on the trajectory and foundational skills associated with children’s ordinality knowledge development.
MATERIALS AND METHODS.
Participants. Eighteen children in kindergarten through third grade were included in the sample. Children were recruited through a departmental database. Participants’ ages ranged from five through eight years of age (five 5-year-olds, five 6-year-olds, seven 7-year-olds, one 8-year-old). Participants were split almost equally by gender (8 males, 10 females). An additional 16 participants were excluded due to issues that prevented the collection of either accurate or full data (e.g., because it was clear that children were randomly guessing, or they were using non-compatible devices with the data collection software).
Procedure. Participants completed a set of four tasks with a researcher over one synchronous Zoom session, lasting approximately 30 minutes. All tasks were created and run through Open Lab, a web application used to help conduct online experimental studies [10]. An experimenter provided directions to children verbally. After the session, the child received a “Junior Researcher” certificate, and the parent(s) received documents with tips on implementing number activities into the home and everyday life.
Four tasks were used to assess children’s magnitude and ordinality knowledge. Two of the tasks were verbal and tested children’s oral number word knowledge (e.g., “one”, “two”, etc.). The other two tasks presented numerals on-screen and tested children’s written numeral knowledge (e.g., 1, 2, etc.). The group of tasks (i.e., number word or numeral) that participants began with was counterbalanced, and the order of the tasks (i.e., magnitude or ordinality first) within each group was randomized. Each task began with two warm-up trials (not included in scoring) with feedback on participants’ answers before moving on to the test trials. In each task, scores were based on the percent of test trials answered correctly.
Verbal Number Word Comparison Task. This task assessed children’s oral number word magnitude knowledge. For this task, the experimenter said two number words, each between one and nine, and the participants were instructed to say which of the two spoken number words was more. The numbers used for the 26 test trials were taken from a previous study [7]. Half of the trials had a distance of 1 through 3 between the digits (e.g., “one” versus “four”) and the other trials had a distance of 4 through 7 between the digits (e.g., “two” versus “seven”).
Numeral Comparison Task. This task assessed children’s written numeral magnitude knowledge. Children saw two single-digit numerals between 1 and 9 on the screen, and the experimenter asked them to click on the numeral that was larger. Note that the researchers did not say the numbers out loud; rather they said, “please click on the number that you think is more.” This task contained the same 26 trials from the verbal number word comparison task, and the structure of each trial was the same. In addition, for all numeral tasks, a fixational cross was presented for 500ms between trials to help the participant know when a different trial would appear.
Verbal Number Word Order Judgment Task. This task assessed children’s number word ordinality knowledge. Children were tasked with judging if a triplet of spoken single-digit number words were in order (e.g., “are the numbers two, three, four in order from smallest to biggest?”). The child provided a verbal yes/no response. After the two practice trials with feedback, there were 32 test trials. These trials also contained multiple sequences of different spacing (e.g., adjacent sequences where all numbers were consecutive when put in order, nonadjacent sequences that skipped numbers in some sort of pattern like “one, three, five” or “two, five, eight,” and unequal sequences that skipped numbers without a pattern like “one, four, six” or “two, four, seven”). In addition, all of the trials that were not in the correct order were in mixed order (e.g., “six, four, nine”).
Numeral Order Judgment Task. This task assessed children’s numeral ordinality knowledge. Similar to previous studies [11, 12], for this task, children saw triplets of single-digit numerals on the screen, and the researcher asked them if “the numbers are in order from smallest to biggest.” Children provided their answer by clicking on either the yes or no button on their screen. This task contained the same 32 test trials from the Number Word Order Judgment Task, and the structure of a trial was the same.
Data Analysis. Task performance was determined based on the percent of test trials that the participant was correct on for each of the four tasks. We conducted correlation analyses to assess the relationship between numeral ordinality task performance with those on the other tasks, when appropriate, by using Pearson correlation coefficients to determine the strength and direction of the association.
Second, given that previous research had suggested that children develop their number word knowledge prior to their numeral knowledge [9], a t-test was also conducted to examine if children’s number word ordinality knowledge was significantly better than their numeral ordinality knowledge. All analyses were conducted using the statistical software JASP [13].
RESULTS.
| Table 1. Performances on the Different Number Tasks | |
| Task Type | Mean (SD) |
| Verbal Number Word Comparison Task | 0.98 (0.03) |
| Numeral Comparison Task | 0.99 (0.03) |
| Verbal Number Word Order Judgment Task | 0.75 (0.19) |
| Numeral Order Judgment Task | 0.69 (0.18) |
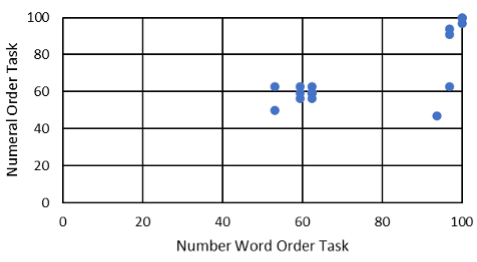
Figure 1. Scatterplot of the Relationship Between Number Word Order Task Scores with Numeral Order Task Scores
Table 1 provides descriptive statistics. Similar to previous studies, participants’ magnitude knowledge on the comparison tasks for both number words and numerals was significantly higher than their ordinality knowledge. In fact, 16/18 children got at most one trial wrong on the number word comparison task, and 16/18 children got at most one wrong on the numeral comparison task. However, because so many participants performed essentially perfectly on the magnitude comparison tasks, there was too little variability in these performances to appropriately find their associations with numeral ordinality performances.
For the one calculated relationship between number word ordinality and numeral ordinality performance, it was found to be strong and significant (r = .75, p < .001). This suggests there is a relationship between children’s number word ordinality and their numeral ordinality knowledge.
In addition, a t-test comparing performance on the number word order judgment and numeral order judgment tasks indicated a significant difference. Children’s number word order judgment performance was significantly better than their numeral order judgment performance (see Table 1), t = 1.88, p < 0.05.
DISCUSSION.
For this study, the research team identified early number skills that may be associated with children’s numeral ordinality knowledge. As previous research had already suggested both relations between magnitude and ordinality knowledge and relations between number word knowledge and numerals, we combined these aspects. Specifically, we examined if there were associations between children’s numeral magnitude, number word magnitude, and number word ordinality knowledge, with their numeral ordinality knowledge. We found a single relation between number word ordinality knowledge and numeral ordinality knowledge, and we found that ordinality knowledge for number words was greater than that of numerals.
Because accuracy had little variability on the magnitude comparison tasks, their relations with ordinality knowledge could not be examined. It is of note that previous work has found a relationship between numeral magnitude knowledge and numeral ordinality knowledge for a sample of children in kindergarten and 1st grade [7, 8]. Thus, it was predicted that this relationship would occur between both numeral and number word magnitude with numeral ordinality in the current study. The incredibly high task scores at the age participants were tested may imply that number word magnitude knowledge may vary more in younger children. Thus, a relationship between number word and numeral ordinality knowledge may be found in younger children who also have more variability in magnitude knowledge. In addition, those with greater magnitude knowledge may be relying on that understanding to aid their numeral order judgments [7, 8]. Nevertheless, it is possible that children, at this or younger ages, may not recruit their magnitude knowledge when making numeral order judgments.
In contrast, this study found a strong correlation between number word ordinality knowledge and numeral ordinality knowledge. In addition, children’s number word ordinality knowledge was found to be significantly higher than their numeral order task performance. One possibility is that children are using their number word ordinality knowledge to develop their numeral knowledge. In particular, children may be using symbol-symbol associations to learn the meaning of Arabic numerals by matching the numeral symbols (e.g., 1) to the “word-symbols” (e.g., “one”) that they have already learned [9]. Together, these findings support the theory that children utilize their existing number word ordinality knowledge in order to further advance their numeral ordinality knowledge. Thus, the results here may support that targeting children’s number word ordinality knowledge may be one way to improve children’s numeral ordinality knowledge.
There are a couple of limitations to this study that may have influenced the current findings. First, this study contained a small sample size, with only 18 participants. Data collection is currently ongoing. More participants collected in the future could bring more validity to the findings as well as more power to detect the hypothesized relationships. Conducting a similar study in-person might also remove a few of the barriers or issues (i.e., tech issues or non-compatibility) that led to the small sample size. In addition, many participants reached the ceiling for the two comparison tasks. Thus, adding more complexity to the comparison tasks (e.g., having participants compare numbers of overall larger value or doing as many trials as possible within a certain time pressure) or testing younger children may shed more light on if there exists a relationship between number magnitude and numeral ordinality knowledge.
There are other ways that this study’s findings can be expanded moving forward. One is to hold an intervention study on how children’s number word ordinality knowledge can help develop their numeral ordinality knowledge. Children can be taught to more explicitly consider the mentioned symbol-symbol associations in order to better link between the two types of number knowledge [9]. In addition, work can be done to explore other number skills that may be associated with numeral ordinality knowledge. One skill that may be related is the successor principle. When children have knowledge of the successor principle, they understand that increasing a set by one moves the quantity to the next number in the count sequence. This knowledge that the spacing between numbers is equal and is always one could be important for children to better grasp the order/organization of numbers. Finally, future work can further explore the transition where children gain a more sophisticated understanding of ordinality. Specifically, it would be informative to test how and when children advance from a “shallow” understanding, which represents an understanding of adjacent-numbered sequences that match the count list (e.g., ‘2 3 4’), to a deeper understanding, which extends this understanding to non-adjacent sequences (e.g., ‘2 4 6’). Because children’s deeper ordinality understanding has been shown to further link with greater arithmetic achievement over just a shallow understanding [11, 12], it is important to examine how children transition from these understandings of numeral ordinality.
Overall, this study found that children may rely on number word ordinality knowledge to help advance their numeral ordinality knowledge. Given the relationship between numeral ordinality knowledge and arithmetic [6, 11, 14], this novel finding advances our understanding of the development of children’s numeral ordinality knowledge and may encourage research to focus on helping teachers develop more effective approaches to ordinality instruction. This research hopes to add to the growing foundation of ordinality research that will allow future researchers to continue exploring how ordinality knowledge develops in children.
ACKNOWLEDGMENTS.
I am grateful for my mentor, Jake Kaufman, and my PI, Dr. Bethany Rittle-Johnson, for guiding me through this research. I would also like to thank the SSMV for this research opportunity, especially Dr. Eeds and my advisor, Dr. Brown, for reviewing my research and supporting me throughout this journey.
REFERENCES
- W. Watts, et al., What’s Past Is Prologue: Relations Between Early Mathematics Knowledge and High School Achievement. Educational Researcher. 43, 352-360 (2014).
- J. Duncan, et al., School readiness and later achievement. Developmental Psychology. 43, 1428-1446 (2007).
- J. Ritchie, T. C. Bates, Enduring Links From Childhood Mathematics and Reading Achievement to Adult Socioeconomic Status. Psychological Science. 24, 1301-1308 (2013).
- L. Rivera-Batiz, Quantitative Literacy and the Likelihood of Employment Among Young Adults in the United States. The Journal of Human Resources. 27, 313-328 (1992).
- F. Reyna, et al., How Numeracy Influences Risk Comprehension and Medical Decision Making. Psychological Bulletin. 135, 943-973 (2009).
- M. Lyons, S. L. Beilock, Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 121, 256-261 (2011).
- Xu, J. LeFevre, Children’s Knowledge of Symbolic Number in Grades 1 and 2: Integration of Associations. Child Development. 92, 1099-1117 (2021).
- E. Hutchison, et al., Extending ideas of numerical order beyond the count-list from kindergarten to first grade. Cognition. 223, 105019-105019 (2022).
- Hurst, et al., Mapping Among Number Words, Numerals, and Nonsymbolic Quantities in Preschoolers. Journal of Cognition and Development. 18, 41-62 (2016).
- Shevchenko, Open Lab: A web application for running and sharing online experiments. Behavior Research Methods. 54, 3118-3125 (2022).
- Gilmore, S. Batchelor, Verbal count sequence knowledge underpins numeral order processing in children. Acta Psychologica. 216, 103294-103294 (2021).
- M. Lyons, et al., Numerical predictors of arithmetic success in grades 1-6. Developmental Science. 17, 714-726 (2014).
- Love, et al., JASP: Graphical Statistical Software for Common Statistical Designs. Journal of Statistical Software. 88, 1-17 (2019).
- M. Lyons, et al., On the ordinality of numbers: A review of neural and behavioral studies. Progress in Brain Research. 227, 187-221 (2016).
Posted by John Lee on Tuesday, May 30, 2023 in May 2023.
Tags: Children, education, Number, Ordinality