A Comparison of Two Algorithms for the Rubik’s Clock

ABSTRACT

In this paper, we compare the two best algorithms for the Rubik’s Clock: 7-Simul and 7-Simul Flip. Both methods have been adopted by world-class clockers and there has been ongoing debate about which algorithm is faster. Using a new formal model for the Rubik’s Clock, we identify a key property of clock scrambles, which enables us to determine the faster method for any given scramble. We then formally derive that 7-Simul is faster than 7-Simul Flip for 74.7% of scrambles, whereas 7-Simul Flip is faster for the remaining 25.3% of scrambles. These findings offer valuable insights for competitive speed clockers, allowing them to adaptively select the optimal method based on the characteristics of a given scramble.

INTRODUCTION.

Invented by Erno Rubik in 1988, the Rubik’s Clock is the most unique puzzle in competitive speedcubing [1]. The clock is a puzzle that consists of 18 dials across both faces, 9 on the front and 9 on the back. Each dial acts like an hour hand of a clock, having 12 possible positions mimicking the 12 hours on a clock. Initially, the dials are scrambled into a random position. The clock is solved when all dials point towards the 12 o’clock marking at the top of each dial as seen in Figure 1. The positions of these dials are changed by turning one or more of the four turn dials on the corners of the puzzle. The clock also has four pins which are either in the up state or down state. These pins determine which sets of dials are affected by the turning of the turn dials.

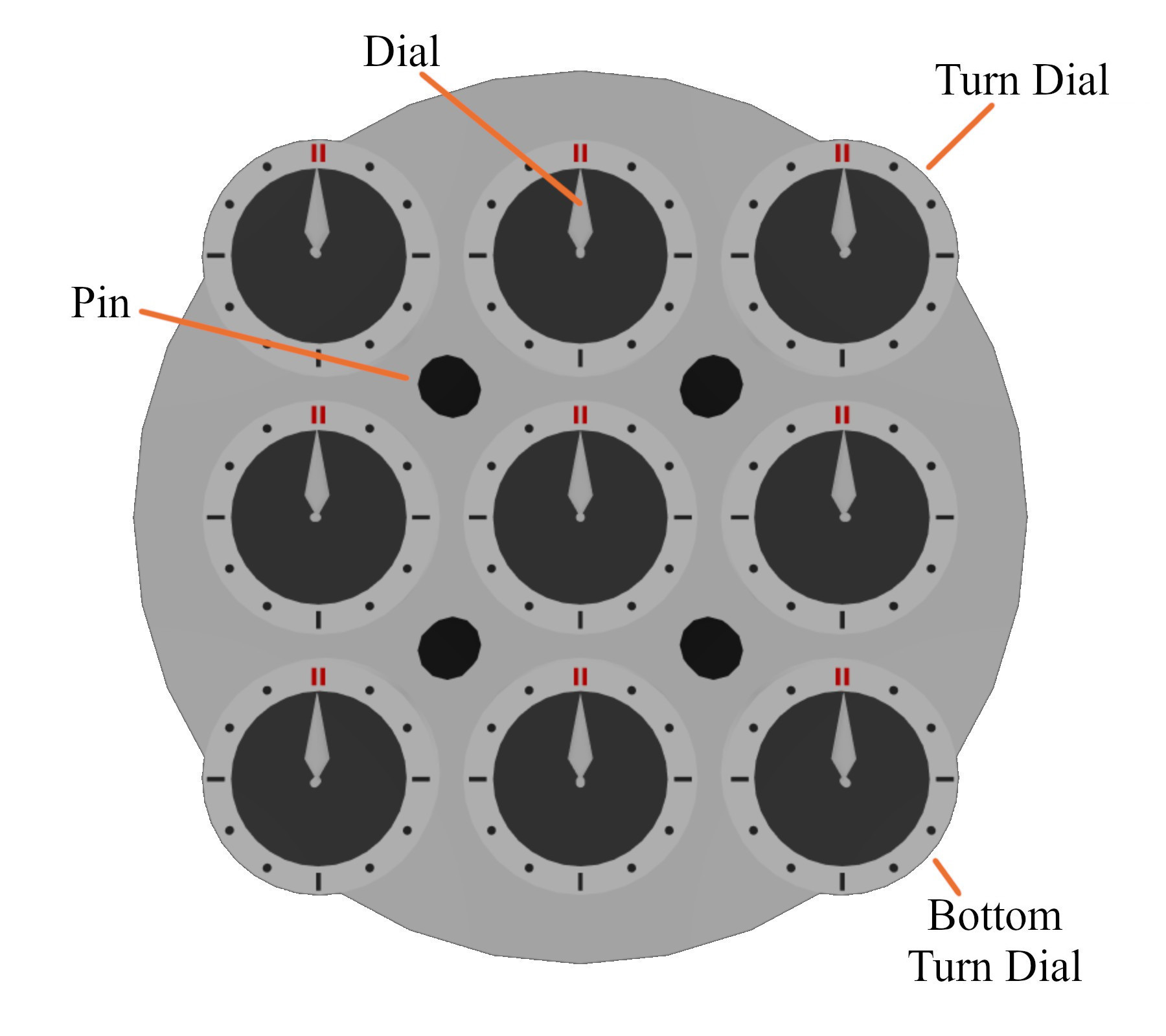
**Figure 1.** One face of the Rubik’s clock in its solved state, with all dials pointing to the 12 o’clock marking. A clock is considered solved when both faces match this configuration.

The clock has traditionally been solved with the Flip Method [2-3]. Improving upon this basic method, a group of clockers including Tommy Cherry invented a method called 7-Simul in November 2022 [4-5]. 7-Simul quickly became the method of choice for leading clockers and was used to set numerous world records. In June 2023, Ben Tibbetts showcased a method with a brand-new idea, adding one aspect of 7-Simul to the Flip method [6]. This idea inspired the invention of 7-Simul Flip in October 2023 by Alexander Moscibroda, Benjamin Paul, Eddie Artze, Fengyuan Lou, and Jaidon Lin as an alternative to 7-Simul, incorporating one aspect of the Flip method while retaining the core structure of 7-Simul [7-8]. Currently, 7-Simul and 7-Simul Flip are the two methods used by world-class clockers. Some scrambles are faster with 7-Simul while others are faster with 7-Simul Flip, and there has been significant debate about which of the two methods is ultimately the better one.

In this paper, we shed fundamental insight into this question. Using a new formal model for clock solves using the 7-Simul and 7-Simul Flip methods, we derive the exact property of a clock scramble that characterizes whether 7-Simul or 7-Simul Flip is faster. By further showing the likelihood at which a random scramble exhibits this property, we can show that 7-Simul is faster for 74.7% of scrambles, while 7-Simul Flip is faster for the remaining 25.3% of scrambles. Our results have practical application for competitive speed clockers. Any clocker who masters both methods may choose to apply the respectively faster method for a given scramble depending on whether the scramble exhibits the property. Indeed, this dual-method approach has recently gained popularity among world-class clockers.

TERMINOLOGY & ALGORITHMS.

Terminology.

In this section we introduce the terminology needed to analyze the algorithms in the later sections. Each change in a dial’s position by one “hour” is called a tick. A move is when one turn dial is turned by any number of ticks, usually with the index finger. A particularly important type of move are d-moves: a d-move is done on one of the two turn dials at the bottom corners of the puzzle. D-moves are done with the pinky finger and require a slight regrip to perform, making them particularly hard and time consuming to execute. For world-class clockers, d-moves typically take 1.2 to 2 times to execute than normal moves. A flip is the act of vertically flipping the whole clock. A flip allows the clocker to see the dials positions on the back face of the clock. A scramble is a random position of dials that is applied to a clock. A solve begins with a scrambled clock and is complete when the clocker turns all dials to the 12 o’clock markings. A solve is carried out in the following manner. First, the clocker has inspection, which is a 15-second period during which the clocker can examine the scramble and plan the moves. After inspection, the clock is placed on its side. Then, the clocker holds down the surface of the timer, releasing it to start the timer. The clocker then solves the clock as quickly as possible. Finally, the clocker presses down the surface of the timer again to stop it.

Algorithms.

Historically, the clock has been solved using the flip method, where one dial is solved per move [2-3]. Out of the 18 dials, the four corner dials on the clock are connected between the front and back face, so there are in fact only 14 individual dials on the puzzle. Since there are 14 dials, the flip method requires a maximum of 14 moves to solve the clock. Although the dials are interlinked, they are grouped and solved in relation to each other, ultimately totaling to only one move per dial to solve the clock. Each move is performed with one hand, and the method is called the flip method because it involves the use of a flip midway through the solve. The flip method requires the clocker to look at the effect of each move to determine the next move. This means the clocker needs visual confirmation of the moves being done, making the solve generally slower as the clocker cannot plan multiple moves ahead.

7-Simul (7s) is a method that consists of a new kind of move: simultaneous moves [4-5]. Simultaneous moves are moves where the clocker executes a move on the front and back face of the clock at the same time on the same combination of pin states. This requires both hands to be used simultaneously for two independent moves. One of the two moves done simultaneously can be a d-move, which makes the overall simultaneous move slower due to the slower speed of performing the d-move. Furthermore, since one of the two moves is done on the back face of the clock, the clocker performs the move without seeing its effects on the dials. The clocker must, therefore, be able to perform a move of any tick number without any visual confirmation. This requires the use of memorization: during inspection, the clocker must plan the solve and memorize a set of numbers associated with the plan that are necessary for the solve. The ability to quickly and accurately do this memorization and perform simultaneous moves is the key to becoming a world-class clocker. Since 2 dials are solved per simultaneous move, one on the front and one on the back, a maximum of 7 simultaneous moves are needed to solve the puzzle using 7s, thus naming the method. Importantly, 7s does not have a flip during the solve. For reasons that go beyond the scope of this paper, each 7s solve contains 0 to 2 simultaneous moves that have a d-move, depending on the scramble. Thus, while 7s is very fast, it can be difficult to execute due to these d-moves.

7-Simul Flip (7sf) attempts to mitigate this difficulty by removing all d-moves, and instead adding a flip in the solve [7-8]. The 7sf method adopts the same principle as 7s with the use of 7 simultaneous moves. The difference between 7sf and 7s is that 7sf begins the solve in a different orientation than 7s, and a flip is added after the first three simultaneous moves. The flip is added after the first three simultaneous moves because in 7s, the d-moves can occur only on moves 1 and 3. Thus, this change eliminates all d-moves to solve the clock at the cost of adding a flip. This also means that for any given scramble the last four moves of 7sf are the same as in 7s. Thus, the key difference important to this paper is that 7s contains 0 to 2 d-moves and no flip, whereas 7sf contains 0 d-moves and 1 flip.

MODEL.

To compare the benefits of 7s and 7sf, we formally define a model for clock solve times. The model captures the solve time as a function of key properties of the scramble, specifically the number of flips and the weighted d-move ticks of a solve.

We define weighted d-move ticks as the number of ticks during d-moves in a solve, with d-moves in the first move being counted double.

The weighted d-move tick metric is defined to roughly correspond with the difficulty of a solve due to d-moves. The reason d-moves ticks during the first move are weighed doubled is because the bottom turn dials are placed on the table at the beginning of the solve. This means they are much less accessible than later during the solve, making a d-move tick during the first move much slower. While the exact weight of first move d-move ticks compared to other d-move ticks depends on the clocker, the multiple of two is used as a common rule of thumb among world-class clockers when discussing the execution of solves.

We introduce a new and original model to calculate clock solve times, which we call the Clock Standard Model. We define the Clock Standard model to calculate the solve time of a given scramble as

\[t=A+x\alpha+y\beta\tag{1}\]

In this model, A represents the time it takes for the clocker to execute all moves of a solve excluding the time for d-moves and flips. x is the number of weighted d-move ticks of the solve. y is the number of flips done in the solve. α represents the d-move addition time which is the incremental addition to the solve time the clocker requires to execute a d-move tick during a simultaneous move. β represents the flip addition time which is the incremental addition to a solve time the clocker requires to execute a flip during the solve.

Notice that y is 0 for solves using 7s and 1 for solves using 7sf. Also, x is always 0 for solves using 7sf. The standard clock model assumes that for a given scramble A is equal when using 7s and 7sf. This is a reasonable assumption as the simultaneous moves 1-3 have the exact same tick number for each hand in both 7s and 7sf, and simultaneous moves 4-7 are the same for 7s and 7sf. The only difference is that 7s simultaneous moves can contain d-moves and those in 7sf cannot, which are separately accounted for using the addition of α in the model.

We define a clocker’s flip-to-d-move (γ) ratio as

\[\gamma=\frac{\beta}{\alpha}\tag{2}\]

The flip-to-d-move ratio captures whether a clocker is relatively faster at executing d-moves or flips. In practice, for a typical world-class clocker, α is in the range 0.07 – 0.1 seconds, β is in the range 0.3 – 0.5 seconds, and A depends on the scramble and can be in the range 1.4 – 2.6 seconds. Given these typical ranges for α and β found among world-class clockers, the median value for α is 0.085 seconds and the median value for β is 0.4 seconds. This means that the median value for γ is 4.706. Given the median for γ, we can assume that most clockers exhibit a normal flip-to-d-move ratio of 4<γ<5.

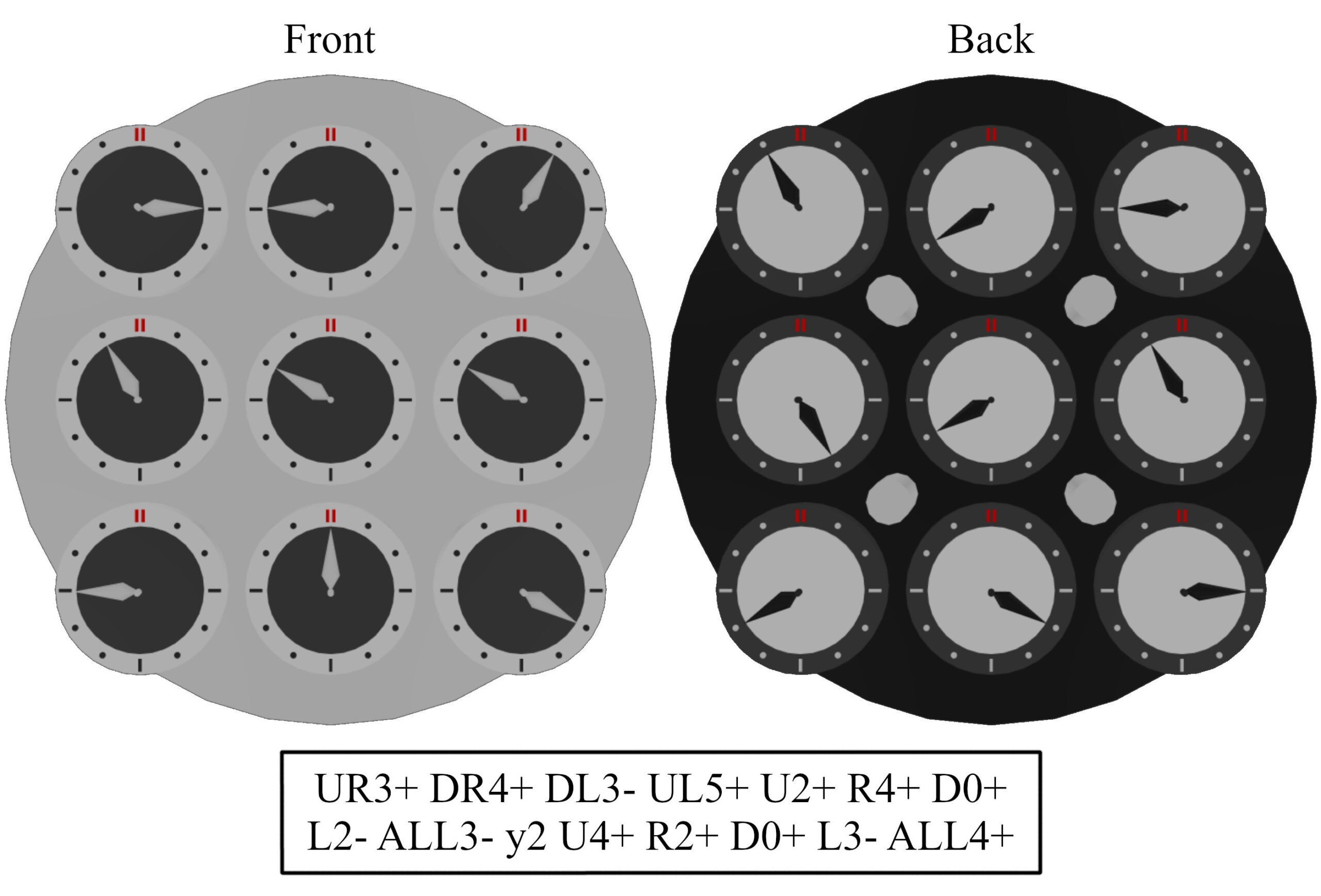
Finally, we define how to model a clock scramble. A clock scramble is a sequence of 14 random moves in 14 different pin configurations. An example of a scramble and its resulting clock faces are shown in Figure 2. The letters (UR, DR, DL, …) represent which pins are pressed up, and the numbers (3+, 4+, 3-, …) correspond to the ticks of the move. Each of these moves is a random number in the range [-5, 6], indicating the number and direction of ticks executed in each pin configuration during the scrambling. For a detailed explanation on clock scrambling, see [9]. With these 14 moves, the clock can be scrambled into all possible random positions of the dials. We can therefore model a clock scramble by generating 14 random integers that make up the sequence of moves for the scramble. We define these scramble numbers as N₁, …, N₁₄, where \(N_i\in\left[-5,\ 6\right],\ \forall i\in\left[1,\ 14\right]\). In other words, the set [N₁, …, N₁₄] defines a specific clock scramble. For the scramble shown in Figure 2 for example, the scramble numbers are \([N_1,N_2,\ N_3,\ \ldots,\ N_{14}]=[3,4,-3,…,4]\).

RESULTS.

For 7s, the number of weighted d-move ticks is the key determinant in how fast a given scramble can be solved. We begin by deriving a formula for the weighted d-move ticks for a given scramble.

Lemma 1: The number of weighted d-move ticks ([N₁, …, N₁₄]) for a given scramble [N₁, …, N₁₄] solved by 7-Simul is

\[x=min\left\{2|N_{10}|+6-|6-{\rm mod}_{12}(N_1+N_4+N_5)|,\\\ 2|N_{11}|+6-|6-{\rm mod}_{12}(N_3+N_4+N_8)|,\\\ 2|N_{12}|+6-|6-{\rm mod}_{12}(N_2+N_3+N_7)|,\\\ 2|N_{13}|+6-|6-{\rm mod}_{12}(N_1+N_2+N_6)|,\\\ 2|6-|6-{\rm mod}_{12}(N_1+N_4+N_5)||+|N_{10}|,\\\ 2|6-|6-{\rm mod}_{12}(N_3+N_4+N_8)||+|N_{11}|,\\\ 2|6-|6-{\rm mod}_{12}(N_2+N_3+N_7)||+|N_{12}|,\\\ 2|6-|6-{\rm mod}_{12}(N_1+N_2+N_6)||+|N_{13}|\right\}\tag{3}\]

Proof: Using 7s, the clock can be solved in eight different orientations. This is because the clock can be held such that the 12 o’clock markings face up, right, down, or left, for both the front and back face of the puzzle. The weighted d-move ticks for a scramble is the minimum of the weighted d-move ticks in each of these eight orientations. For each orientation, the ticks of the two d-moves in a 7s solve are determined by two specific tick differences. We define a tick difference to be the difference in dial position, measured in ticks, between two specific dials. The number of ticks of the first d-move is determined by the tick difference between the center and bottom edge dial on the front face in the initial orientation. The number of ticks of the second d-move is determined by the tick difference between the center and top edge dial on the back face. For any given orientation, these two tick differences form pairs. Each pair of tick differences has two orientations: one orientation where the first tick difference determines the first d-move and one orientation where the first tick difference determines the second d-move. Given the eight possible orientations, there are four pairs of such tick differences.

The ticks of the d-moves can be determined as a function of these tick differences, and therefore can be expressed as a function of the initial scramble values N₁, …, N₁₄. Each tick difference can be found by adding up the scramble values of all scramble moves that turn the center dial, but not the corresponding edge dial. This calculates the total ticks of all moves affecting only one of the two dials, thus resulting in the tick difference. By thus considering moves that only affect the center for each tick difference in each pair, the following four pairs of tick differences are found: \((N_1+N_4+N_5,\ N_{10})\), \((N_3+N_4+N_8,\ N_{11})\), \((N_2+N_3+N_7,\ N_{12})\), and \((N_1+N_2+N_6,\ N_{13})\). Each of these pairs represents the total number of ticks required to perform the two d-moves for a given orientation.

We now derive the weighted d-move ticks for a scramble using these four pairs. For each tick difference, we calculate the d-move ticks executed by the clocker. D-move ticks are in the range [0, 6] as that is the maximum number of ticks in any direction that needs to be turned for any move. For the four tick differences with the form N, the d-move ticks are simply |N|. For the tick differences that follow the form N_x+N_y+N_z, the d-move ticks can be expressed as \(|6-|6-{\rm mod}_{12}(N_x+N_y+N_z)||\). Since our definition of weighted d-move ticks doubles the d-move ticks in the first move, these four pairs of tick differences turn into eight combinations, one for each tick difference in a pair being the first d-move of a solve. This accounts for the eight orientations possible in a solve. For one expression, the form N is multiplied by two and for the other expression, the form N_x+N_y+N_z is multiplied by two. Finally, taking the minimum of these eight expressions results in the weighted d-move tick value x for a given scramble.

In practice, the previous Lemma implicitly assumes that the clocker is able to find the optimal orientation for the solve during inspection. This is a reasonable assumption as a world-class clocker is easily able to identify the best orientation and do its memorization during inspection. This means that when executing a solve using 7s, a clocker will solve it from the orientation that results in the optimal weighted d-move ticks.

Lemma 1 shows that the weighted d-move ticks for a given scramble can be calculated purely based on the scramble numbers N₁, …, N₁₄.The weighted d-move ticks for a given scramble determines how fast the solve is using 7s. This means that for a given scramble, we can determine which method is faster. Scrambles for which the weighted d-move ticks are low are faster with 7s than 7sf, and scrambles for which the weighted d-move ticks are high are faster with 7sf than 7s. Ideally, this allows the clocker to decide on the better method for a specific scramble during inspection.

Thus, to determine the percentage of scrambles that are faster with each of the two methods, we calculate the distribution of weighted d-move ticks for random scrambles. The following lemma (see Figure 3) shows the distribution of weighted d-move ticks for random scrambles.

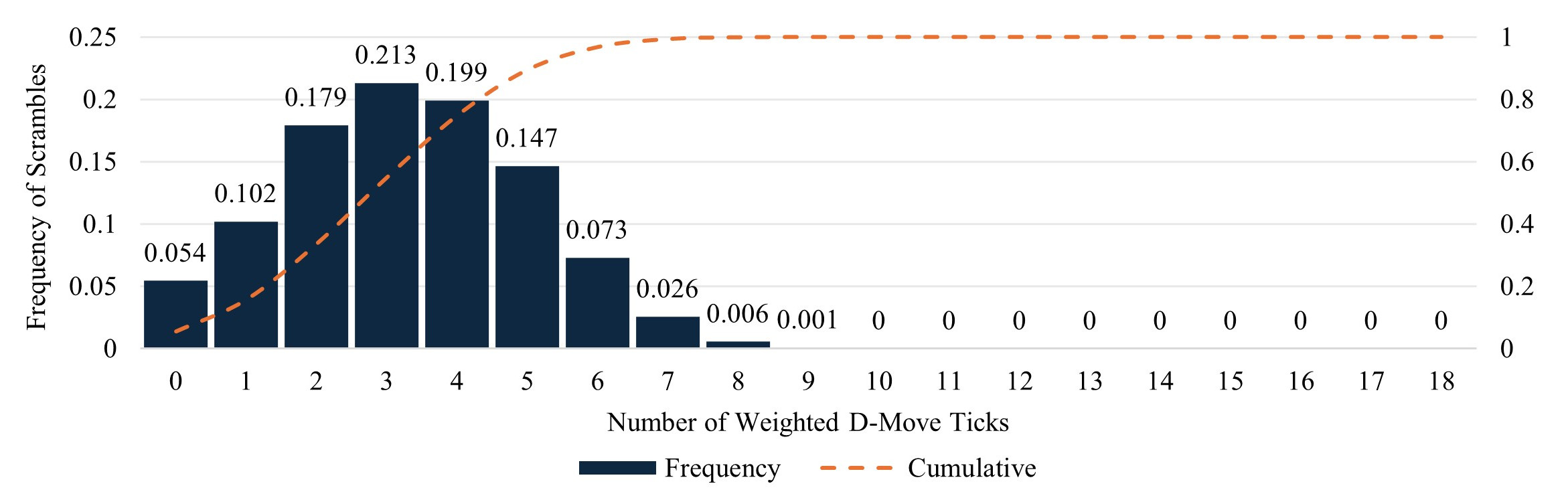
**Figure 3.** Distribution of weighted d-move ticks (x) of random scrambles. The blue bar graph shows the frequency of scrambles with specific weighted d-move tick counts, which can range from 0 to 18. The orange line shows the cumulative frequency of scrambles with weighted d-move ticks from 0 to the given value.

Lemma 2: The weighted d-move ticks (x) of a random clock scramble follows the distribution

\[[0.054,\ 0.102,\ 0.179,\ 0.213,\ 0.199,\ 0.147,\ 0.073,\ 0.026,\ 0.006,\ 0.001,\ 0,\ \ldots,\ 0]\tag{4}\]

Proof: We model a clock scramble as described in the Model section by generating 14 random ordered integers in the range [-5, 6] and labelling them N₁, …, N₁₄. For each scramble, we then calculate the weighted d-move ticks using Lemma 1. Repeating this for 1,000,000,000 randomly generated scrambles, we find the distribution shown in Figure 3.

Having found the distribution of the weighted d-move ticks, we now establish which method is faster as a function of the weighted d-move ticks of a scramble.

Theorem 1: 7-Simul is faster for all scrambles where the weighted d-move ticks (x) is x<5, and 7-Simul Flip is faster for all scrambles where x≥5.

Proof: A solve using 7s contains anywhere between 0 and 18 weighted d-move ticks and no flip. A solve using 7sf instead consists of no weighted d-move ticks and one flip. Therefore, the clock standard model for 7s and 7sf can be represented as \(t=A+x\alpha\) and \(t=A+\beta\), respectively, where x is the number of weighted d-move ticks. Hence, for any given scramble, if xα<β, 7s is faster than 7sf and if xα>β, 7sf is faster than 7s. Given that most clockers have a normal flip-to-d-move ratio of 4<γ<5, the clocker’s ratio is 4<β/α<5, and thus 4α<β<5α. It follows that if x<5 for a given scramble, then xα<β and the solve is faster with 7s. If x≥5 for a given scramble, then xα>β and the solve is faster with 7sf.

Next, we combine Lemma 2 and Theorem 1 to derive the main theorem of the paper, namely the percentage of scrambles faster with 7s and 7sf, respectively.

Theorem 2: 74.7% of all possible scrambles are faster with 7-Simul, while 7-Simul Flip is faster for the remaining 25.3% of scrambles.

Proof: Lemma 2 and Figure 3 show the distribution of weighted d-move ticks for a random scramble. The probability that x<5 is the combined sum of the probabilities that \(x\in\left\{0,\ 1,\ 2,\ 3,\ 4\right\}\) since a given scramble has only one possible weighted d-move tick value. The sum of these probabilities is 74.7%. Since x is in the range [0, 18], the probability that x≥5 is \(1-P(x<5)\) which is 25.3%. It follows from Theorem 1 that the 74.7% of scrambles where x<5 are faster with 7s than 7sf, and the other 25.3% of scrambles where x≥5 are faster with 7sf than 7s.

CONCLUSION.

In this paper, we have analyzed the difference between 7-Simul and 7-Simul Flip for solving the Rubik’s clock. We have shown how the solve time of a scramble fundamentally depends on the weighted d-move tick variable. Using our equation for the weighted d-move ticks x, we can determine for every scramble which of the two methods is faster. Analyzing the properties of a random scramble, we further show that 7-Simul is faster for 74.7% of scrambles where x<5 and 7-Simul Flip is faster for 25.3% of scrambles where x≥5.

The invention of 7-Simul Flip has affected the solving methods of many world-class clockers. With practice, world-class clockers are able to determine whether a scramble has x<5 or x≥5 within the first few seconds of inspection. Accordingly, the clocker can choose the faster method and use the remaining inspection time for memorization. Although 7-Simul is still the primary method for many world-class clockers, others including Carter Thomas have established records using both methods, adjusting the method depending on the given scramble during inspection. In this paper, we provide the theoretical underpinning for this new dual-method, or method-neutral, approach to clocking. We expect that in future years, this method-neutral approach will further gain in popularity among world-class clockers.

REFERENCES.

C. C. Wiggs, C. J. Taylor, “Mechanical puzzle marketed as Rubik’s Clock” (Patent EP0322085, 1989).
J. Denes, G. L. Mullen, “Rubik’s Clock and Its Solution,” Mathematics Magazine 68, 378–381 (1995).
D. Taylor, L. Rylands, Mastering Rubik’s Clock: The Solution to Rubik’s Latest Puzzle (Simon & Schuster, 1988).
T. Cherry, “We invented a FASTER Clock method,” YouTube, 27 November 2022; available: https://youtu.be/Hm2VSKBvl5c. [Accessed 13 November 2024].
T. Cherry, “7 Simul Tutorial (Clock) by Tommy Cherry,” YouTube, 27 January 2023; available: https://youtu.be/ZX5ssGWUGb4. [Accessed 4 April 2025].
B. Tibbetts, “Potentially good clock method,” YouTube, 31 May 2023; available: https://youtu.be/_ZqXAFsQPwY. [Accessed 13 November 2024].
E. Artze, J. Lin, F. Lou, A. Moscibroda, B. Paul, “Complete 7simul-flip Tutorial (3 versions),” Google Docs, 8 October 2023; available: https://docs.google.com/document/d/1Ep5uxcrYpEdVcZnnN_m_hVc04OXaIYgD1C0fHx3hxVE. [Accessed 4 April 2025].
J. Joshi, “Tommy V2 – Advanced 7-Simul Flip Tutorial (Clock),” YouTube, 9 August 2024; available: https://youtu.be/A1iUwpWzyXw. [Accessed 4 April 2025].
A. Walker, “How to Scramble Square-1, Megaminx, and Clock [WCA],” YouTube, 7 July 2017; available: https://youtu.be/h84rbhXmIRQ. [Accessed 4 April 2025].

Posted by buchanle on Tuesday, June 24, 2025 in May 2025.

Tags: 7-Simul, 7-Simul Flip, algorithm, Rubik’s Clock, Rubik’s Cube