A Proposal for Optimal Emergency Vehicle Routing using Quan-tum Annealing

ABSTRACT

Algorithms used for routing emergency vehicles tend to be computationally intensive. With millions of road networks and even more traffic configurations, widely used routing algorithms, such as Dijkstra’s algorithm, rely on statistical approximation to select best routes given the time and resource complexity of the problem space [1]. The advent of quantum computing hardware allows us to produce superior algorithms to solve similar problems. For instance, prudent use of quantum parallelism can help explore a vast array of alternate routes while accounting for various routing constraints in real-time [2]. This paper introduces an iterative approach to implement a quantum routing algorithm for emergency vehicles. This algorithm seeks to improve route selection by exploring all possible shortest paths across any two points in a geographical area while accounting for specific constraints along each route, in real-time, using a process called quantum annealing [3]. The objective is to find the fastest route given start and end location in a geographical network, while simultaneously accounting for multiple constraints such as traffic incidents or road closures along the way.

INTRODUCTION.

Ambulances and other emergency vehicles provide a crucial service to our communities. Given their critical nature it is vital that they have a navigation system that constantly evaluates current traffic conditions and provides the quickest way to their destination. Every second matters, and it can mean the difference between life and death.

Traditional routing algorithms, such as Dijkstra’s and A* algorithms used in Google Maps, can consistently find the shortest path between any two points in a geographical area [4]. However, scaling these algorithms when there are many alternate routes remains a challenge. Modern computers run on digital architecture, using binary bits for information processing. These bits can only exist in two states, 1 or 0, and only allow a limited solution space to be explored in parallel at any given time. Therefore, they will not scale well when dealing with a large network of roads under a set of dynamic, real-world constraints that impact the optimal route. Quantum computing solves this issue by using subatomic particles, such as electrons, for information processing [5]. These particles possess a unique property to exist in multiple states at once, what is often referred to as a superposition of entangled states [6]. This allows the quantum computer to explore a vast set of possible solutions, in parallel, and choose the best solution, simultaneously accounting for a multitude of constraints.

This paper highlights a proposal to improve emergency vehicle routing using a technique called quantum annealing. The term ‘annealing’ comes directly from metallurgy, where a metal is heated, and allowed to slowly settle into a stable configuration when cooling. Similarly, quantum annealing utilizes the superposition of quantum bits and their entanglement to explore a vast set of possible alternate routes simultaneously. Starting from a high energy state of superposition, when each quantum bit exists in multiple states at once, the annealer evaluates and compares the relative costs of each route against all others, gradually allowing the bits to settle into a low energy state, which corresponds to the optimal route. A mathematical model called a Binary Quadratic Model (BQM) is used to formulate the problem and submit it to the annealer. ‘BQM’ is an umbrella term for solving optimization problems with quadratic functions acting on binary variables by minimizing costs involved [6]. A BQM is a concise way to specify the interactions between various nodes (points of interest such as intersections, traffic signals, etc.) and edges (roads between nodes) of the network. The annealer uses the BQM to determine the relative costs associated with choosing a specific route.

The annealer runs on a quantum processing unit (QPU) which utilizes quantum bits (qubits). The qubits are initialized into a superposition of all possible states with equal probabilities to create a set of viable routes. This is the initial state of the system. Next, the annealer analyzes the relative costs of each route as compared to all other possible routes using a phenomenon called quantum tunneling, in which a continuous wavefunction is used to define all possible solutions [3]. The objective of the annealer is to find the global minima for this wavefunction. This corresponds to the lowest energy state within the system. The global minima represent the best route given a set of unique constraints.

MATERIALS AND METHODS.

Accessing Map Data.

The road network data of the city of Haslet, TX, accessed via OpenStreetMap was used to test the algorithm. The road network consists of nodes that are intersections or points of significance within the city. The edges represent the roads connecting adjacent nodes. Each edge has an associated weight, corresponding to time taken to traverse the edge.

Finding the Optimal Route.

The objective of the algorithm is to find the fastest route between any two arbitrary nodes given a set of constraints represented as weights on the edges. For this experiment, a traffic incident is simulated by marking a set of nodes as unnavigable. These are tagged as ‘incident nodes.’ Consequently, the edges adjacent to these marked nodes are assigned higher weights.

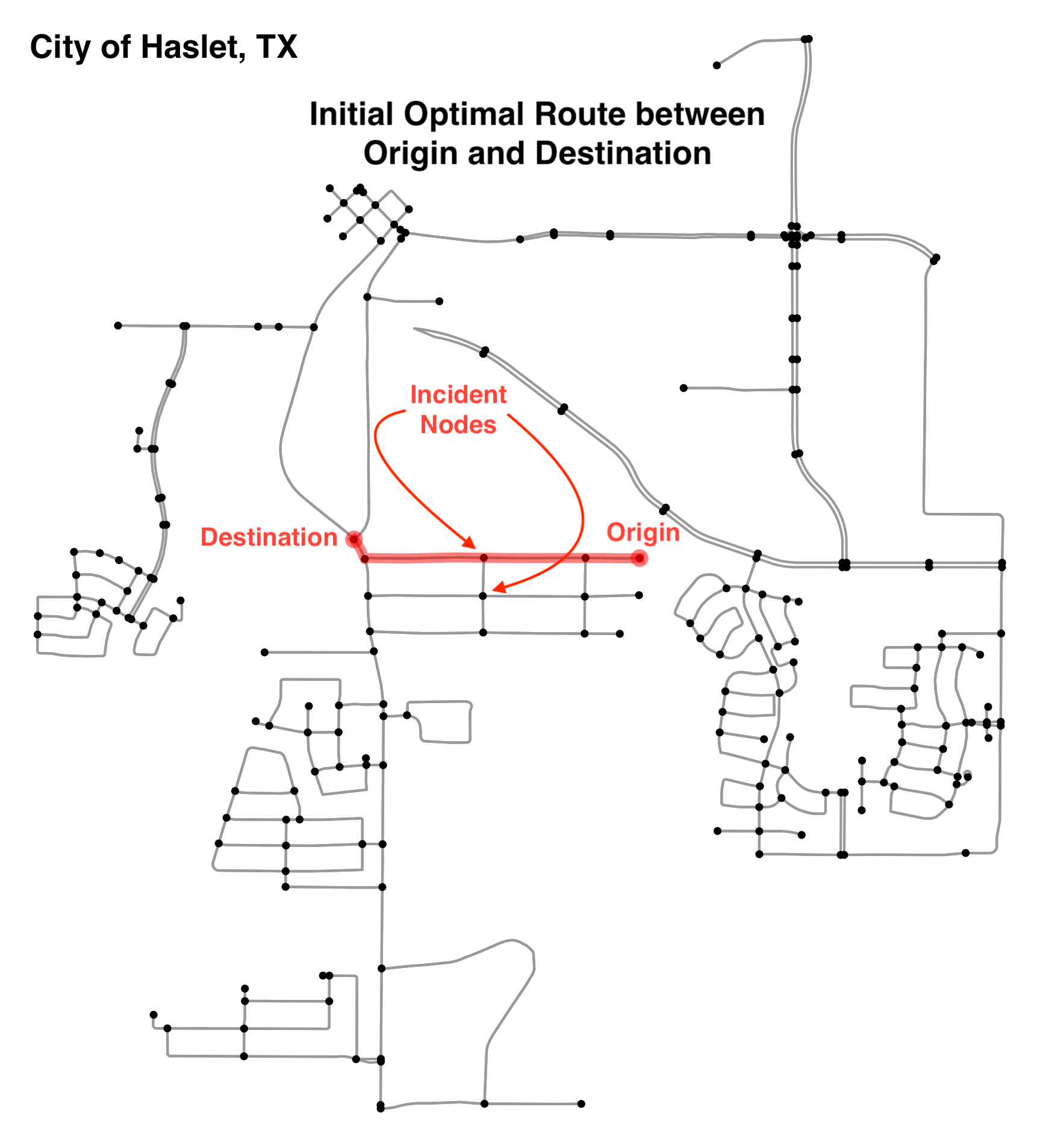
The algorithm finds alternate shortest routes that do not touch the marked nodes. Figure 1 depicts the unconstrained shortest path between the start and end nodes from the road network. The nodes marked with the red arrows represent two randomly selected incident nodes along the shortest path. Dijkstra’s Algorithm was used to establish the initial shortest path between the two selected nodes. Dijkstra’s Algorithm initially sets the weights of all nodes except the starting node to infinity. It then updates the edge weights of the nodes that can be traveled to directly from the starting node. Next, it compares the weights and picks the shortest route. After that, the node with the shortest route from the starting node is now set as the new starting node. Finally, Dijkstra’s Algorithm iterates through this process until the shortest route is achieved all the way to the target node [1].

A BQM is then employed to find the constrained shortest route. Different costs are assigned within the BQM to describe how “expensive” a certain route is. For example, routes along the incident nodes are assigned higher weights corresponding to the severity of the incident. This allows the algorithm to consider all possibilities of how the vehicle can be routed, while minimizing travel time.

BQMs have two parts, a linear and a quadratic term. The linear term represents the cost and benefits of each decision made, modeled by a binary variable multiplied by a constant. The quadratic term represents the interaction between binary variable pairs, modeling the effect of various routing decisions between any two nodes. The BQM’s objective function is a summation equation that sums various costs across all alternatives. Achieving optimization would minimize the result of this function. It can be generally represented as:

\[E\left(x\right)=\sum_{i}{h_ix_i}+\sum_{i<j}{J_{ij}x_ix_j\ }\tag{1}\]

where   represents the linear coefficients,  represents the quadratic interactions between binary variables  and . In the next step, penalties are added. Penalties are large constants that are responsible for placing higher costs on infeasible solutions, forcing the algorithm to lean towards more feasible solutions. In other words, they bring the quantum model from a high to low energy state, the latter being the optimal solution [7].

The Advantage_system4.1 quantum annealer accessed through D-Wave’s Leap Quantum Cloud Service was used to process the BQM during initial development. However, due to the difficulty of procuring sustained access to the annealer, a local simulator was used instead. This essentially simulates the annealing process and sends jobs to the user’s local computer, making it a much more accessible alternative. D-Wave’s Python-based Ocean SDK was used to create and submit the model to the annealer.

Experiment.

Given the OpenStreetMap data for Haslet, Texas, two arbitrary nodes were designated as start and end nodes. Dijkstra’s Algorithm was used to find the baseline shortest route between these nodes, as shown in Figure 1.

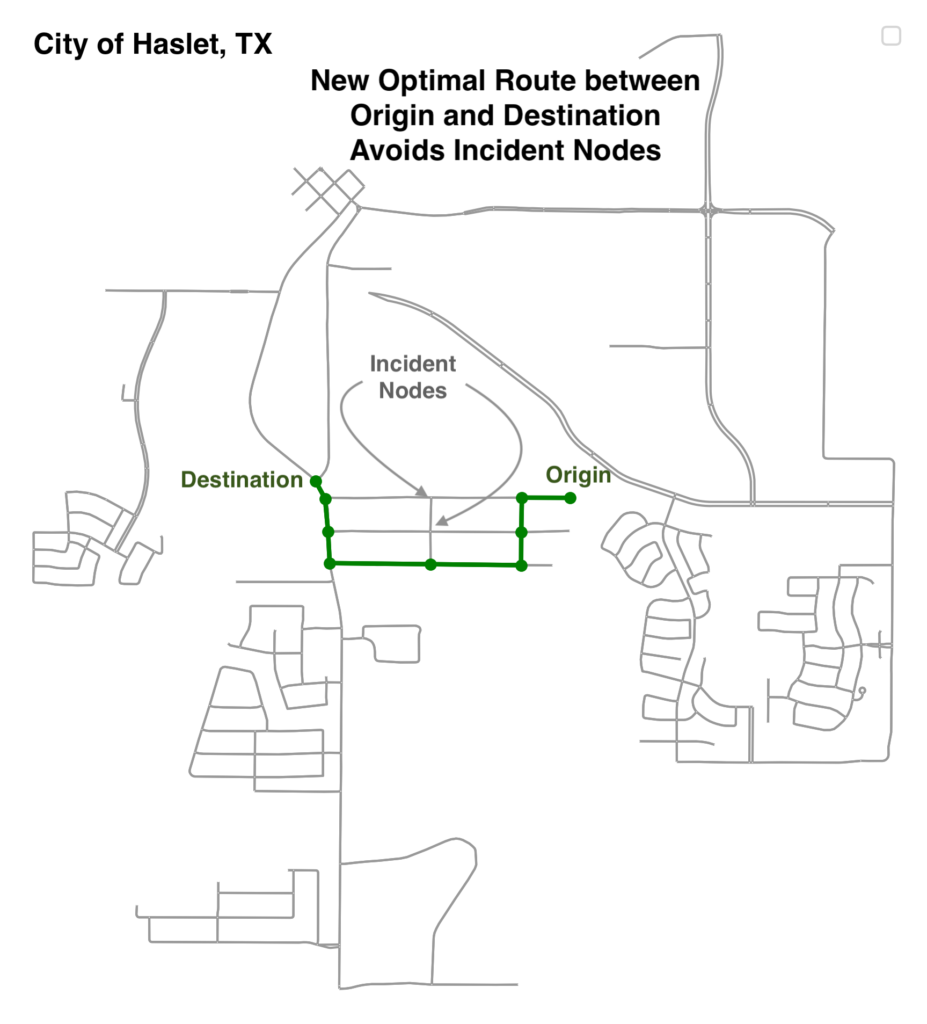
A traffic incident was simulated by marking two nodes along this shortest path as unreachable. Next, a BQM was created using a data frame of all the nodes and travel times to their immediate neighbors along the shortest path. BQM constraints were established by adding large penalties to the incident nodes, to reduce the chances of the annealer choosing them as part of the optimal solution. Ideally, in a real-world scenario, the penalties would be proportional to the severity of the incident(s). Additional penalties involving start, end and neighboring nodes along the established optimal path were also formulated to account for single incoming and outgoing edges. In addition, penalties that enforced the connectivity of nodes along a path were also enforced to prevent an invalid final route map. To improve the validity of results, the BQM is run multiple times, each with a different combination of penalty constants that influence which constraints are prioritized over others. This helps the solver come up with a well-rounded solution that balances the importance of each constraint. Finally, a frequency-based consensus algorithm is used to aggregate the results. The algorithm iteratively counts the number of times a node appears in the solution set and divides it by the total number of solution-sets to generate the percentage of solutions containing the node. The final solution set consists of nodes that appear above a high threshold percent of solutions. The threshold can be adjusted depending on the density of the city map and the nature of the objective function. This allows the algorithm to either return a single consensus-based route or simultaneously explore multiple optimal routes. Figure 2 shows the revised optimal path between the two nodes. As expected, the new route carefully circumvents both incident nodes from the initial unconstrained shortest route.

Testing the limits of the algorithm.

To truly test this algorithm’s limits, the above experiment was run on a variety of possible routes. Specifically, the algorithms processed routes with 16, 26, and 55 nodes between the selected start and end nodes. On each of these paths, the BQM was run for 27, 64, 125, 216, and 343 iterations. The results from these iterative tests are captured in Table 1 below and Figures S1-S3, with the aggregated results across all three routes summarized in Figure S4. In all cases, the BQM generated solutions satisfied all the constraints, as well as circumvented the incident nodes.

RESULTS.

A moderately sized subgraph with 55 nodes only took ~5.7 seconds to compute the optimal route vs. ~1.6 seconds for a small 16-node subgraph as seen in Table 1 below. This is ideal for local optimization across a small region. A notable observation was that across all path sizes, the quantum routing algorithm generated the valid solution within only 27 iterations, and the extra iterations proved to be redundant. However, high density areas might require more iterations.

Table 1. BQM Performance Statistics
# Nodes between start and end locations	# Edges along all routes	# Nodes in solution	# of BQM iterations	Time Elapsed in seconds
16	20	13	27	1.5881
16	20	13	64	3.5629
16	20	13	125	6.8406
16	20	13	216	11.7200
16	20	13	343	18.4846
26	29	25	27	2.7649
26	29	25	64	6.1961
26	29	25	125	12.0257
26	29	25	216	20.5257
26	29	25	343	32.4110
55	57	54	27	5.6806
55	57	55	64	12.9482
55	57	55	125	24.9433
55	57	55	216	43.0541
55	57	55	343	67.8292

DISCUSSION.

The results of this experiment were as expected; the BQM supplied the constraints to the annealer, and the annealer consistently found the shortest route within 27 iterations. The results were validated by running Dijkstra’s Algorithm on the graph with the incident nodes deleted. The shortest route thus produced matched exactly with the BQM solution. Interestingly, for certain routes, the BQM generated multiple optimal paths, as their relative weights were equal. Future experiments will focus on obtaining and utilizing real-time traffic data as constraints to the model. These include modeling complex scenarios such as count of vehicles at traffic signals, average speed of vehicles along each edge and other such impacts due to traffic incidents. This allows the algorithm to dynamically pick the best alternative.

ACKNOWLEDGMENTS.

I would like to thank Dr. Sergii Strelchuk, Royal Society University Research Fellow, University of Cambridge, and Mr. Sean Harvey from the University of Bath for guiding me through the research process as part of CCIR’s Future Scholars Program.

SUPPORTING INFORMATION.

The Python code used to simulate the experiment can be found as Exhibit S5 in the supporting information document along with data and visualization presented throughout this paper.

REFERENCES.

1. Ray, Quantum Simulation of Dijkstra’s Algorithm. International Journal of Advance Research in Computer Science and Management Studies 2, 30-43 (2014).
2. Neukart, G. Compostella, C. Seidel, D. von Dollen, S. Yarkoni, B. Parney, Traffic Flow Optimization Using a Quantum Annealer. Front. ICT 4, 29 (2017).
3. D-Wave Systems. “What is Quantum Annealing?”. Accessed July 19, 2024. https://docs.dwavesys.com/docs/latest/c_gs_2.html
4. Says, The Algorithms Behind The Working Of Google Maps, CodeChef (2021). Accessed January 9, 2025. https://blog.codechef.com/2021/08/30/the-algorithms-behind-the-working-of-google-maps-dijkstras-and-a-star-algorithm/.
5. International Business Machines. “What is Quantum Computing?” Accessed June 15, 2024. https://www.ibm.com/think/topics/quantum-computing
6. MIT Technology Review. “Explainer: What is a quantum computer?”. Accessed June 15, 2024. https://www.technologyreview.com/2019/01/29/66141/what-is-quantum-computing/
7. D-Wave Systems. 2022. “Problem Formulation Guide”. Accessed August 17. 2024. https://www.dwavesys.com/media/bu0lh5ee/problem-formulation-guide-2022-01-10.pdf.
8. Toth, D. Vigo, The Vehicle Routing Problem (Society for Industrial and Applied Mathematics, 2002).
9. Sahil, S. Jain, J. Hamdard, QUANTUM PATHFINDERS: NAVIGATE THE SHORTEST ROUTE. International Journal of Engineering Applied Sciences and Technology 7, 116-121 (2022)
10. Khadiev, L.I. Safina, Quantum Algorithm for Shortest Path Search in Directed Acyclic Graph. Moscow University Computational Mathematics and Cybernetics 43, 47-51 (2018).
11. R.S Aghaei, Z.A. Zukarnain, A. Mamat, H. Zainuddin, A Hybrid Algorithm for Finding Shortest Path In Network Routing. Journal of Theoretical and Applied Information Technology 5, 360-365 (2009)

---

---

Posted by buchanle on Thursday, June 19, 2025 in May 2025.

Tags: Binary Quadratic Model, Dijkstra’s Algorithm, Quantum Annealing, Quantum Processing, Routing Algorithm