Assessing the viability of qiskit and IBM Quantum to solve QUBO problems with publicly available quantum computers

ABSTRACT

This paper explores a specific optimization problem called the aircraft loading optimization problem. It is an optimization problem that can benefit from a quantum speedup by a quantum computer. This problem can benefit from a quantum speedup because it is part of an optimization class called QUBO problems. These problems can be expressed as a matrix-vector product. Quantum computers can convert this matrix into an Ising Hamiltonian and then perform quantum annealing to solve it. Unfortunately, these quantum computers are expensive and inaccessible, so this paper attempts to solve the aircraft loading optimization problem on accessible quantum computers or quantum simulators, using quantum-classical hybrid solvers. We used qiskit optimization to set up the problem and then tried multiple ways of solving it. The first was to simulate a quantum computer on our local hardware with qiskit, which inevitably failed because the problem was too large for the qiskit simulators. The second attempt was to use qiskit runtimes with IBM Quantum. This also failed because the packages were not compatible with qiskit optimization, making medium-size QUBO problems unsolvable by open-source quantum computing.

INTRODUCTION.

In aviation, one of the known areas that can benefit from a quantum speedup is optimization. Quantum computers are particularly good at specific optimization problems because the superposition of qubits and their ability to perform quantum tunneling can be used to find the minimum state of the problem. One practical optimization problem in aviation is the aircraft loading optimization problem. The problem states: if you have ‘N’ objects and ‘M’ spaces in an aircraft, what is the optimal way to load the objects so the aircraft can still fly at maximal capacity? This problem falls under a classification of problems called Quadratic Unconstrained Binary Optimization (QUBO) problems. Due to their setup, QUBO problems lend themselves very well to solutions via quantum computers. This is because QUBO problems belong to the complexity class ‘NP’, meaning that the time taken to solve these problems can be expressed as a polynomial function of the number of variables in the problem if and only if solved by a nondeterministic Turing machine, which is a quantum computer. In other words, NP problems require quantum computers to solve. Typically, these quantum computers are expensive and inaccessible, so this paper aims to answer whether publicly available quantum computers, such as those at qiskit or IBM, can solve a twenty-five variable aircraft loading QUBO optimization problem. For low-variable problems, classical computer annealing may be powerful enough to find the optimal solution. As the problem size increases, classical annealing cannot handle the size of the problems, making quantum annealing and quantum-classical hybrid algorithms become appealing when the problems become bigger.

A QUBO problem is a binary optimization problem. The problem is set up by defining some function of binary variables (variables that can only be 0 or 1) and optimizing this function. QUBO problems must be quadratic or linear and subject to no constraints. They appear in the form:

\[Minimize/Maximize: y=\overrightarrow{X}^TQ\overrightarrow{X}\tag{1}\]

where ‘X’ is a vector containing all binary variables, and Q is a matrix representing the coefficients of the linear and quadratic terms in the equation [1]. Most QUBO problems are first expressed as a typical function of variables, then they are rewritten into the vector form. The linear terms in the function can be mapped to the diagonal of the matrix, while the off-diagonal values refer to the quadratic terms. These QUBO matrices can come in two forms: upper right triangular and symmetrical. If the matrix had an upper right triangular form, the quadratic binary variable 5 · X(1) · X(2)would have a value of 5 in column 1 and row 2, which corresponds to (1, 2); if the matrix had a symmetrical form, though, the matrix would have an integer of 2.5 in (1, 2) and (2, 1) [1]. This works because when multiplying out the matrix-vector products, they are equivalent statements.

Frequently, QUBO problems are not initially expressed in vector form, but rather as a typical equation of binary variables. Then, we can factor out a vector of binary variables and its transpose to get the matrix ‘Q’. An example of what a simple QUBO problem might look like is below.

\[y=2X(1)+4X(2)-6X(1)X(2)\tag{2}\]

Where X(n) are the binary variables. To convert this to a matrix, we can leverage the property that these are binary variables, and they can only take on the values 0 and 1, meaning that \(X(n)=X(n)^2\). Once we do this, we can factor out the variable vector and its transpose. This gives us the equation:

\[y=\begin{bmatrix}X(1) & X(2)\end{bmatrix} \begin{bmatrix}2 & -3\\-3 & 4\end{bmatrix} \begin{bmatrix}X(1)\\X(2)\end{bmatrix}\tag{3}\]

Multiplying out the matrix-vector product will yield equation 2, meaning they are equivalent statements. This matrix contains the linear terms of equation 2 on the diagonal with the quadratic terms occupying the off-diagonals.

Although QUBO problems must be unconstrained, it is frequently useful to encode a constraint into the problem. Computer scientists have gotten around the unconstrained nature of QUBO problems by converting a constraint into a quadratic penalty function. The process is like Lagrange multipliers from Lagrangian mechanics in that you scale the constraint and subtract it from the main equation. The key difference between Lagrange multipliers and QUBO penalty functions is that the QUBO constraints must be changed into a new form by introducing more variables before they can be scaled and subtracted. Initially, QUBO constraints look something like this:

\[X(3)-X(2)>0\tag{4}\]

To convert this to a QUBO solvable format, it must be converted to a penalty function [1]. The process of making a penalty function is not the purpose of this paper since qiskit has a function that converts constraints into penalty functions, so we will not get into it. By subtracting the penalty function from the original equation before converting to matrix-vector form, the information of the constraint can be encoded into the problem by causing the equation to reach a higher value if the constraint is not met, meaning the minimum solution will not be found if the constraint is not met [2]. The conversion from equation form to vector form should only be done after subtracting the penalties because if not, the constraints will not be encoded into the problem.

QUBO problems have a large capacity for quantum speedup because the matrix can be expressed as an Ising Hamiltonian, which is a matrix containing the spins of many different electrons to code for information. Quantum computers can then optimize problems by using these Ising Hamiltonians and quantum annealing. The most common optimization tool is a quantum annealer, a specific quantum computer that can only solve optimization problems. These are typically 15 million dollars, but they can solve problems with 1 million variables and over 100,000 constraints. Quantum annealers use superposition probabilities to tunnel through the potential energy peaks to find a global minimum. Since these are very expensive, the alternative is a Quantum Approximate Optimization Algorithm (QAOA), a hybrid quantum-classical algorithm approximating the optimal solution using a less powerful quantum computer and a classical computer that communicate together to find the solution to the Ising matrix. This is the ideal optimizer for a medium-sized QUBO problem because classical annealers are not equipped for their size, but quantum annealers are too expensive for their benefit to the medium problem size. Quantum-classical hybrid algorithms are also accessible: they can be simulated on a local system or exported to a quantum computer to run externally, meaning anyone with local hardware can use them.

MATERIALS AND METHODS.

The aircraft loading optimization problem has a simple minimization function because it is linear; the variables are scaled values of X(a, b) where ‘a’ and ‘b’ are integers [2]. If the minimized value of this variable is ‘1’, object ‘a’ should be loaded into space ‘b’; however, if the minimized value of this variable is 0, it means that object ‘a’ will not be put into space ‘b’ [2]. Objects can have varying masses and take up different amounts of space, with some taking a half-space, others taking a whole space, and others taking 2 spaces. The overall function to minimize becomes:

\[Minimize: y=-\sum_{a=1}^n \sum_{b=1}^m t_am_aX(a,b)\tag{5}\]

Where “a” is the object number, is the mass of object a, “b” is the occupying space number, and:

\[\begin{cases} t_a=1 & \text{if object a takes 1 or 1/2 space} \\ t_a=\frac{1}{2} & \text{if object a takes 2 spaces} \end{cases}\tag{6}\]

Constraints will be utilized to ensure the structural integrity, the center of mass position, and the plane’s lift collectively do not stop the plane from functioning. Constraints will also be used to stop physical geometry from being broken, such as 2 objects in 1 space when they each take up 1 whole space.

The no-overlaps condition ensures that there are no overlaps within the spaces. This means that there won’t be multiple boxes in the same space unless they both have a size of half a space. The constraint follows:

\[\sum_{a=1}^n d_aX(a,b) \leq 1 \\ \begin{cases} d_a=1 & \text{if object a takes 1 or 2 spaces} \\ d_a=\frac{1}{2} & \text{if object a takes 1/2 space} \end{cases}\tag{7}\]

Next, we constrain our equation so that each object does not occupy multiple spaces:

\[t_a\sum_{b=1}^m X(a,b) \leq 1 \\ \begin{cases} t_a=1 & \text{if object a takes 1 or 1/2 position} \\ t_a=\frac{1}{2} & \text{if object a takes 2 positions} \end{cases}\tag{8}\]

The final geometric constraint that we must add ensures that objects that should occupy 2 spaces actually occupies 2 spaces, rather than just 1. The constraint equation follows:

\[\sum_{b=1}^{m-1} X(a,b)X(a,b+1)=1\tag{9}\]

Rather than converting the constraints to penalty functions manually, qiskit can be used to convert them faster and more conveniently. Additionally, qiskit has a built-in function where it converts QUBO equations into Ising matrices, so there is no need to go into how that is done in this paper.

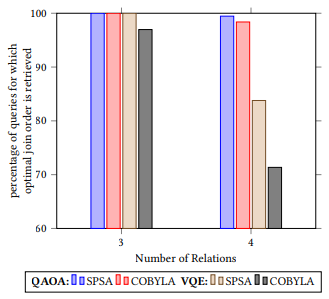
Once qiskit has converted the problem into an Ising matrix, all that remains is the solution. Quantum computers can compute these quickly and efficiently. Out of all quantum computers, quantum annealers and simulators outperform any other method of solving QUBO problems [3], but they are unrealistic for most people. We will use a quantum-classical hybrid optimizer to test their viability of solving this problem. Figure 1 shows the effectiveness of each quantum-classical hybrid optimizer, where the Y-axis is how often the optimizer finds the ideal solution, and the X-axis corresponds to the complexity of the problem. Out of the accessible quantum-classical solvers, the most accurate solution method was a QAOA using an SPSA optimizer (Figure 1). Despite this, the COBYLA optimizer is a better choice for the specifics of this problem because it takes less time/processing power at higher dimensional computation [3]. Because of this, we will use a QAOA with a COBYLA optimizer to ensure the best results.

RESULTS.

We tested this code before adding the structural and flight constraints but even this reduced code caused a problem. The error message from qiskit said that the matrix we were trying to solve was 2.25 quadrillion dimensional, requiring 32 petabytes of RAM. After researching, we discovered this was because of how qiskit interacted with our local system. Their method for converting QUBO equations to Ising matrices was not designed for problems as large as the one we are trying to solve. In response, we tried using qiskit runtimes to send our code to a public quantum computer, but this also failed. We attempted to solve the problem on local hardware with fewer variables; we reduced the number of spaces and objects to 3, resulting in a 9-variable equation with several geometric constraints. This was successfully computed, even on our local hardware. Still, the solution took over a minute, suggesting that 9 variables are on the verge of what is solvable on local hardware with qiskit.

DISCUSSION.

Qiskit could be an excellent alternative to quantum annealers since it is free and accessible to anyone who owns a classical computer, but qiskit is currently not advanced enough to solve a medium-sized aircraft loading optimization problem. The way they simulate quantum gates on classical hardware makes them ineffective for medium-size problems. Even the 25-variable problem we tried was unsuccessful. Though the 9-variable problem we tried was successful, most realistic problems are greater than 9 variables, so Qiskit’s simulated QAOA is not powerful enough to solve real-world problems. This was why we then tried using a QAOA through qiskit runtimes, which uses public quantum computers at IBM Quantum as the quantum part of the QAOA. This allows qiskit runtimes to have access to substantially more computing power than qiskit on a local system would. Qiskit runtimes also did not work because qiskit started migrating their runtimes packages but has not yet migrated their quadratic problem package. This makes it impossible for the necessary functions to communicate with each other effectively and thus leaves this problem unsolvable by qiskit runtimes. If qiskit were to finish their migration, qiskit runtimes might be able to solve the 25-variable aircraft loading optimization problem but more research is needed to know for sure. The next step to allow bigger QUBO problems to be solved is for IBM Quantum to add a quantum annealer backend. By adding this, they would eliminate the need for a QAOA altogether because we could just use quantum annealing to find the solution with open-source quantum computers.

The advancement of quantum computing will benefit everyone. This is because classical computers struggle to run programs that fall into the NP-hard difficulty class, such as QUBO problems. Quantum computers do not. The development of quantum computers could open entirely new areas of research that are unreachable by classical computers. In addition, programs solvable by classical computers could get a quantum speedup, which means that the time computers take to run programs could decrease. If local hardware improves, or IBM Quantum adds a quantum annealer backend, tools like qiskit would become viable for solving realistic QUBO problems. Publicly solvable QUBO problems would save businesses the money that they would spend buying a quantum computer because they could do it for free online.

CONCLUSION.

Publicly available QAOAs are not yet viable for solving the aircraft optimization problem. Generally, publicly available QAOAs cannot yet solve complex QUBO problems subject to multiple constraints. To solve these problems, qiskit runtimes needs to finish migrating all its packages so the quantum computers at IBM Quantum can run more powerful QAOA’s and solve medium-sized QUBO problems. Additionally, IBM should add a quantum annealer as a backend because it will eliminate the need for a quantum-classical hybrid optimizer altogether. Optimization is one of the domains most subject to quantum speedup; having a quantum annealer backend would benefit people looking to get into quantum optimization. A public quantum annealer backend could become the mainstream method of solving the aircraft loading optimization problem in higher dimensions or even QUBO problems in general.

SUPPORTING INFORMATION.

The exact code used for optimization can be found in the supporting information document.

REFERENCES.

Glover, G. Kochenberger, Y. Du, Quantum bridge analytics i: A tutorial on formulating and using QUBO models. A Quarterly Journal of Operations Research. 1, 1-14 (2018).
Pilon, N. Gugole, N. Massarenti, Aircraft loading optimization – QUBO models under multiple constraints. Arxiv preprint arXiv:2102.09621. 1, 1-8(2019).
Nayak, J. Rehfeld, T. Winker, B. Warnke, U. Çalikyilmaz, S. Groppe, Constructing optimal bushy join trees by solving QUBO problems on quantum hardware and simulators. BiDEDE ’23. 7, 1-7 (2023).

Posted by buchanle on Thursday, May 2, 2024 in May 2024.

Tags: Ising model, linear algebra, qiskit, Quantum Computing, QUBO