Evolution of Light and Heavy Quarks in Simulated Electron-Proton Collisions

ABSTRACT

Intrinsic charm is significant to proton stability because the mass of the charm quark is greater than the proton itself, which implies that protons can remain stable in unusual configurations. Studying intrinsic charm will bring much-needed insight into charm quark dynamics and shed light on the mechanism of proton stability. Unfortunately, current methods for identifying the occurrence of intrinsic charm are time consuming and expensive. Therefore, this study sought to simulate and identify phenomena unique to intrinsic charm events which can be used to identify intrinsic charm occurrence. Utilizing open-source physics simulation software, this study simulated 10,000,000 electron-proton collisions which contained a charm quark and produced a jet. Using an energy-energy correlator to measure the amount of charmed meson pairs versus strange meson pairs in the jets there was an observed modest excess of pairs of charmed mesons in the high transverse momentum jets at small angles when compared to pairs of strange mesons. Both groups return to similar distributions at large angles. This indicates that intrinsically charmed protons become symmetrically biased at specific energies during quark ejection.

INTRODUCTION.

Physics at the subatomic level is studied primarily with the use of particle colliders. Currently, most of these colliders collide 2 of the same kind of particle, such as proton-proton or lead nuclei with another lead nuclei. These kinds of colliders have answered many physics questions and will continue to be useful for the foreseeable future, however they leave many undesirable uncertainties when attempting to study individual particle constituents.

Electron-ion collisions are much better at studying the constituents of a single particle due to the characteristics of the electron [1]. In an electron-ion collision, all observed collision products except for the scattered electron can be identified as daughter particles of the ion with 100% confidence due to the electron being an indivisible particle. Because of this unique trait, electron-ion collisions are of great interest to physicists wishing to study the constituents of individual protons and heavy atomic nuclei [1]. Unfortunately, at the time of writing there are no operational electron-ion colliders in the world. Currently, the construction of the Brookhaven National Laboratory Electron-Ion Collider is underway and is being funded by the US Department of Energy, with the completion of the facility forecasted in the early 2030’s. This means that research wishing to exploit the advantages of electron-ion collisions must be done with simulations for the time being.

Of particular importance to the study of individual protons is investigating proton stability, which is determining whether protons naturally decay. This is significant because if protons are found to decay, it means that matter is inherently unstable, and all matter will eventually decay. Currently all research into proton stability has indicated that protons are stable, however the exact reasons why they remain stable is a mystery. Proton stability studies have fallen off in frequency in recent years as the methods used to test it have been gradually exhausted. However, a recent study indicated that charm quarks ejected from the proton are occasionally found more than their antiparticles (symmetry breaking), resulting in a net positive production [2]. This is a significant development for proton stability research as it provides a new way to investigate the mechanism that keeps the proton stable in unusual configurations. Unfortunately, physics currently lacks a conclusive description of the dynamics of net positive intrinsic charm events due to a lack of data on the topic.

The goal of our study was to identify an observable sensitive to intrinsic charm dynamics from simulated electron-proton collisions and recommend it for measurement with data from the future Electron-Ion Collider, with the hopes that its employment will return useful information for the study of proton stability. Our study sought to find a reliable indicator of intrinsic charm occurrence in collisions to reduce the amount of time and effort needed to reach the conclusion that an intrinsic charm event has occurred.

Directly studying the charm quark is not viable in a simulation, as it would not be reproducible in a real detector due to colour confinement. However, it is possible to instead study the D mesons that the charm quark hadron sizes into when ejected from the proton, which solves the colour confinement problem and allows the simulation to be reproduced in real detector experiments. D mesons are therefore the primary marker for charm quark dynamics studies.

To better understand the behavior of the charm quark, it will need to be compared to a known control. In this study, the strange (s) quark will be used for comparison. Both the strange quark and the charm (c) quark are second generation quarks, which means they are frequently produced together and have similar properties to the “normal” first generation quarks (up and down, which normally make up the proton at rest). For example, the charm quark has the exact same electric charge and spin as the up quark, but their masses differ by a large amount. Because of this, charm quarks can substitute an up quark in any composite particle (see Figure 1).

When quarks are ejected from their parent particle, they do not exist freely due to confinement [3] [4]. Confinement is a feature of quantum chromodynamics, a governing theory of quarks and gluons. Confinement, also known as hadronization, occurs when quarks and gluons convert into hadrons (2 or more quarks paired together with binding gluons) [4] [5] [12]. With a lone quark, the most common end product of hadronization is a meson [4] [5]. When a quark hadronizes into a meson, it pairs with an antiparticle that was created from the remnants of the collision [4] [5]. This meson then carries the combined properties of the 2 quarks it is made of. Charm quarks hadronize into a D meson, and by studying the D meson inferences can be drawn for both the properties of the charm quark and the dynamics of intrinsic charm. To compare what is observed for the charm quark, results will need to be compared to a more thoroughly described particle. The particle chosen for this purpose was the K meson, which is made of a strange-anti-up quark pair. K mesons share properties with D mesons, as they are both second generation quarks and are both massive quarks. However, they do have unique differences. K mesons are much more common in collisions than D mesons due to their low mass (~0.494GeV) which requires very little energy to be taken from a collision to form (this energy is known as a potential-energy barrier). This potential-energy barrier is small compared to D mesons (mass ~1.867GeV, roughly 3.8 times more than a K meson). Therefore, comparing D mesons with K mesons will reveal properties and behavior unique to the D meson and by extension, the charm quark.

MATERIALS AND METHODS.

This study used the collision simulation program PYTHIA [13] (version 8.3) to generate simulations of eP collisions at 10+100GeV. Additionally, CERN’s C++ ROOT [14] package and the FastJet package [6] were used for data handling and jet analysis, respectively. Mesons are unstable and decay rapidly due to their particle-antiparticle configuration. To effectively study D and K mesons, the decays of D⁰, D⁺, D⁻, K⁰, K⁺ and K⁻ were prevented from occurring. For computing efficiency, the minimum Q^2 (Q^2 is the amount of energy deposited into the proton by the electron from the force of the collision) was set to 15 GeV to reduce the amount of “wasted” collision events the simulation would produce (if Q^2 is below the mass of the mesons being studied, they likely won’t be produced at all). Of all the particles in the event, the ones that were analyzed were only final state particles, meaning they were at the end of their decay process and had reached stable configurations (except for the K and D mesons).

PYTHIA simulates collision events using a model based on the current Standard Model of particle physics (SM) and utilizes Monte-Carlo techniques (random sampling) from known expected values to obtain a result from a set of given parameters. PYTHIA uses random number generation to define variables for each collision, which produces statistically accurate models when performed with many events. To get the best possible statistical accuracy, 10 million collisions were simulated.

Energy-Energy Correlators (EEC’s) are a useful tool which were previously limited by technological capabilities but have recently been improved and refined by physicists to be able to accurately display phenomena that were previously beyond the reach of detectors [7] [8] [9] [10]. They allow researchers to infer the evolution of the particles in a jet during their travel between the collision point and the detector. Physicists can analyze the jet particles when they reach the detector to deduce the dynamics of the collision and the particles it produced [12].

Program.

PYTHIA, FastJet, ROOT and other packages are imported to the program and defined as callable objects. Collision parameters are defined as a 10+100GeV ep collision, D and K meson decays are forced off. The number of events n is set to 10,000,000. The program steps are as follows.

1. Collision Simulation

PYTHIA 8.3 simulates one 10+100GeV ep collision and generates all the data for the event. 1 is subtracted from n.

2. Jet Identification.

FastJet analyzes the collision data from step 1 (Collision Simulation) and determines if a jet (radius 0.4) was created. If FastJet detects a jet, the collision data is saved alongside the jet properties, which are appended to a 4-vector array. If FastJet doesn’t find a jet with a transverse momentum above 5 GeV, the data from the collision is discarded and 1 is added to n to compensate.

3. Event Loop (L₁).

Steps 1 (Collision Simulation) and 2 (Jet Identification) are repeated in a loop named L₁. Once n = 0 the PYTHIA collision event generator is stopped, and all collision jet data is saved as a vector array. L₁ is terminated.

4. Jet Tagging (L₂, F₁).

Loop L₂ takes all the jets identified in L₁ and passes them through filter F₁. Filter F₁ identifies jets containing at least one particle with a mass in the range of a D meson or a K meson. Jets that fit this description are “tagged” for analysis (F₁’) and all others are discarded.

5. Jet Grouping (L₂, G₁).

All tagged jets from F₁’ are passed through transverse-momentum (P_T) grouper G₁, which identifies tagged jets with PT values between 5-10 (low P_T) and 10-15 (high P_T). Tagged jets matching these values are saved to their respective P_T group as G₁’ and any tagged jets outside of these ranges are discarded. L₂ is then terminated.

6. Energy-Energy Correlator (L₃, E’).

In loop L₃ an EEC (denoted as E) is calculated for each jet from G₁’. The output of the EEC (E’) is then placed into the high P_T or low P_T group. A ROOT graph canvas is filled with E’ of the respective P_T group. L₃ is then terminated.

\[EEC=\frac{1}{\sum_{Jets}\sum_{i\neq j}\frac{E_iE_j}{P_{T,Jet}^2}}\frac{d\left(\sum_{Jets}\sum_{i\neq j}\frac{E_iE_j}{P_{T,Jet}^2}\right)}{d\left(\Delta R\right)}\tag{1}\]

An energy-energy correlator is a function that measures the dispersion of particles as a function of their energy. If there is a pair of particles within a jet that have a similar energy level, then they are grouped by this function and marked as having a correlation with each other. The equation sums every jet’s individual particles and compares them to another particle within that jet to the jet’s PT and produces a numerical expression of their correlation with respect to how far they are separated from each other as a function of the jet radius (ΔR).

7. Data Representation

The ROOT canvas pads containing the final EEC data grouped by high and low P_T are drawn as histogram graphs and saved to a .root file containing all the raw data in case later analysis is needed.

RESULTS.

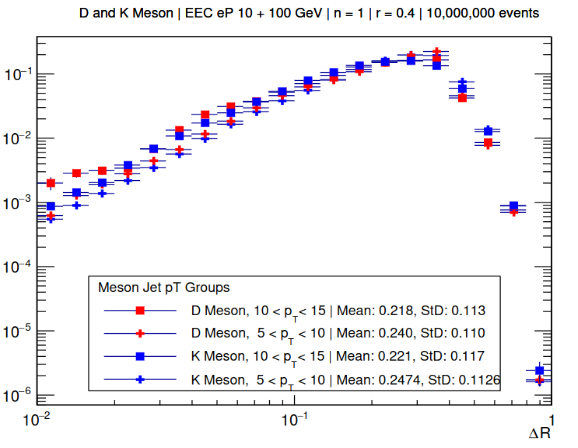
The EEC function showed that K mesons have a linear increase in the number of correlated P_T pairs from a small ΔR until reaching a ΔR associated with post hadronization. This was also true for the D mesons; however, the high P_T D meson had a “levelling off” in the number of pairs from a ΔR of 10^-2 to ~10^-1.8. Additionally, the high PT  D meson pairs were more common at the crossing point from hadronization to stable pairs.

DISCUSSION.

The Energy-Energy Correlator produced several observables useful for describing intrinsic charm behavior. There is an excess of D meson pairs compared to K meson pairs at small ΔR values. The established understanding of K mesons being more common than D mesons due to their mass is contradicted by Figure 2. This is because of the selection bias of the study focusing only on collisions which involve a struck charm quark in the proton, resulting in D mesons being found in every collision. In real collisions, charm quarks (and therefore D mesons) are rarely found, which is why physics currently describes K mesons as being more common (because strange quarks are much lighter and therefore easier to produce).

This contrast is the result of the intended design of the study, which ignored the majority of real-world cases (which did not have charm quark) and only examined the minority cases which involved a charm quark with the aim of identifying unique phenomena which could be associated with intrinsic charm. Consequently, if a real collision observed an excess of D meson pairs compared to K meson pairs at the correct ΔR values, that collision can be tagged as having a charm quark.

D mesons are commonly paired with K mesons when they are produced from a collision with a charm quark.

The relatively low energy of the collision (center of mass energy 90 GeV) indicates that the D meson is commonly paired with the K meson at small ΔR values.

An excess of D meson pairs versus K meson pairs post-hadronization (above ΔR=0.4) was not observed in Figure 2. The sharp drop-off of particle pair counts beginning around ΔR = 0.4 is because of the selected size of the jet radius. The jet radius was set to 0.4, and at ΔR of 0.4 the measurement boundary transitions from space where most of the particles in the jet are found to sparsely scattered particles at the extremities. These particles are equivalent to outliers and have a much smaller sample set, resulting in the sudden drop in the number of pairs. This effect combines with the 0.4 point being the location that hadronization ends, creating a sudden shift in the data.

 

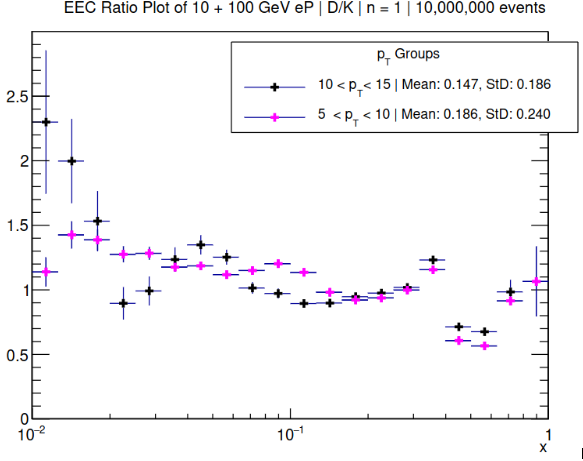
There is a distinct characteristic of the EEC for D meson pairs compared to K meson pairs which could be used to identify charm quark collisions in real data.

This positive ratio of D mesons to K mesons at the specific ΔR in the EEC shows potential as a signature for detecting intrinsic charm and should be tested with real collisions. If this “signature” can successfully identify intrinsic charm events in real collisions, it would be a major improvement in current intrinsic charm detection methods which are extremely time consuming.

Furthermore, determining whether the signature remains distinct with more common mesons should be done, as it could possibly prove to be more reliable and flexible than only in application to K mesons. A likely candidate for this research would be pions, as they are nearly universal in any collision.

Further research should also investigate the potential for the signature to be of a general type, and not specifically matching the one found in this paper. If so, the variations in EEC signature could tell physicists different things about the dynamics of the collision.

The K meson distribution could possibly substitute the D meson distribution for detectors which cannot or are not detecting D mesons.

The distribution of the K mesons represents the 2-point energy-energy correlator of K mesons in an intrinsic charm event. If a detector is attempting to study intrinsic charm or randomly happens to produce an intrinsic charm event, the distribution of the K mesons may be used as a substitute for the D meson signature if the detector is not able to detect D mesons or is not reliable for heavier mesons. This feature of the results may be applied to detectors at facilities other than the upcoming EIC [1] [10] that have randomly produced an intrinsic charm event.

The K meson signature can be used to identify the intrinsic charm event with data that is more likely to be captured, as detectors may be more likely to record K meson data than D meson data, depending on the type and research goal being conducted. This concept can be used to retroactively identify intrinsic charm phenomena secondary to the research goal of the detector using collected data. This would increase knowledge of the dynamics of intrinsic charm overall through the ability to identify its occurrence in detectors which are not specifically researching intrinsic charm.

Unfortunately, this will be a less reliable method and should be paired with D meson distribution, if possible, as the results obtained in this study indicate that intrinsic charm events have a unique difference in the D and K meson distributions. Additionally, the distribution of the K meson is much more uniform and lacks the distinctive disruption found in the D meson distribution, making it difficult to distinguish from normal K meson distributions. Removing the D meson distribution removes half of the unique phenomena found in this study.

The goal of this study was to identify any phenomena that could be distinctively attributed to intrinsic charm events using simulated electron-proton collisions. By studying the simulated jet structures and applying energy-energy correlators to the collision products, the simulations identified a distinct statistical feature of these correlators which indicated an effect of intrinsic charm.

Utilizing these distinctive phenomena will aid in identification and study of intrinsic charm events in real collision data studies. By searching for the energy-energy correlator signatures present in the results, the computing time to identify intrinsic charm events in data will be reduced considerably.

Further research should be conducted with other simulation models such as HERWIG and SHERPA. Obtaining a signature from all these models and then combining them into one averaged metric will give the best possible signature to use for real data analysis.

This study found statistical features of EECs of charm quark events and could be used in real collision data analysis. However, charm quark events are extremely rare, and optimal use of these data features will be difficult to achieve in the first few applications. Identifying the possible range of signatures and the ways in which the simulated data differs from real data is vital to the effective employment of the signatures in charm quark related data analysis.

A possible limitation of my research project is the fact that current physics datasets may be unreliable, since simulated conditions can be controlled in a manner that real world physics cannot be. This means that the models may need to be adjusted or calibrated to fit real data, to compensate for variations in detector accuracy and possible discrepancies in detector energy. A way this could be done is to run this study on another simulation program such as HERWIG and compare results.

Another potential issue is the fact that intrinsic charm dynamics are currently poorly understood, meaning that simulated dynamics could be entirely inaccurate. However, the current practical method for predicting phenomena is to run simulations, which is by nature only as reliable as the accuracy of the model, which cannot be determined in this instance because of lack of a real EIC or hard data on intrinsic charm. The task of predicting unknown phenomena must be approached in some way, and simulations are currently the best option.

Additionally, the sample size of 10 million for the simulations will need to be compared with other independent results, which could have large differences in signature due to the relatively small sample size. This study should be run again under identical conditions with a larger sample size, ideally around 1 billion, although 100 million would be enough to improve the accuracy of the signature.

ACKNOWLEDGMENTS.

Thank you to the School for Science and Math at Vanderbilt for providing me with the opportunity to work on this project. Special thanks to Dr. Rithya and Ben Kimmelman for their time and willingness to work with me on this project. Thank you to Jussi Vinikaiinen for their help with revising my draft and their amazing work on energy-energy correlators. Thank you to all RKE group graduate and undergraduate students that I worked with who let me join lab meetings and ask them questions.

REFERENCES.

1. R.A. Khalek et al., Science requirements and detector concepts for the electron-ion collider: EIC yellow report”, Phys. A 1026 (2022).
2. NNPDF Collaboration, Evidence for intrinsic charm quarks in the proton. Nature 608, 483–487 (2022)
3. Particle Data Group, “Standard Model of Elementary Particles”, (2019);
4.  S. Marzani, G. Soyez, M. Spannowsky, Looking inside jets: an introduction to jet substructure and boosted-object phenomenology. arXiv.1901.10342 [High-Energy Physics -Phenomenology] (2022).
5.  A. Larkoski, Jet physics from the ground up. arXiv.2112.15122 [High Energy Physics – Phenomenology] (2021).
6.  FastJet User Manual, CERN-PH-TH/2011-297 (2024).
7. H.T. Li, Y. Makris, I. Vitev, “Energy-Energy Correlators in Deep Inelastic Scattering”, Phys. Rev. D 103, 094005 (2021).
8. A. Tamis, “Measurement of Two-Point Energy Correlators Within Jets in p+p collisions at √s = 200 GeV”, (Hard Probes Meeting, 2023).
9. D. Neill, G. Vita, I. Vitev, H.X. Zhu, “Energy-Energy Correlators for Precision QCD” (US Community Study on the Future of Particle Physics, Snowmass, 2021).
10.  Z. Yang, Y. He, X.N. Wang, “Probing the short-distance structure of the quark-gluon plasma with energy correlators, arXiv DOI (2023).
11.  Z. Tu, “ePIC: Status & Plans” (RHIC/AGS Users Meeting, 2024).
12. Andronic, P. Braun-Munzinger, K. Redlich, J. Stachel, Decoding the phase structure of QCD via particle production at high energy, arXiv DOI (2018).
13. J. Altmann, C. Bierlich, N. Cooke, N. Desai, PYTHIA, version 8.311, PYTHIA (2019);
14. R. Brun, F. Rademakers, ROOT – An Object Oriented Data Analysis Framework, Proceedings AIHENP’96 Workshop, Lausanne, Sep. 1996. Version 6.32.00.

---

---

Posted by buchanle on Friday, June 20, 2025 in May 2025.

Tags: Electron-Ion, Jets, Proton, simulation