Exploring Methods of Manipulating and Optimizing the Cell Potential of Zinc-Copper Cells: Anion Effects, pH Variations, and Supplementary Electrolyte Effects

ABSTRACT

Efforts to find alternatives to lithium batteries due to safety and environmental concerns have focused on alternative models that can facilitate better safety, lower costs, and more ideal performance. Constructing rechargeable zinc-copper cells has been a point of focus in many research initiatives due to its high capacity, simple synthesis method, environmental friendliness, and low cost. Effective Zn-Cu batteries require controlling voltage-related factors. This study evaluates three different anions (Cl^–, NO₃^–, SO₄^2-) bonded to Zn/Cu at various molar concentrations, pH’s, and in circumstances of added supplementary electrolytes. The study intends to evaluate these factors in terms of their relationship with cell potential both theoretically and experimentally. The study’s findings suggest that at varying zinc concentrations, divalent anionic species exhibit a lesser rate of deviation from the standard cell potential (1.10V) than monovalent anions. Moreover, the study finds that the Debye Hückel model remained effective at concentrations less than 10^-3 M while the Davies model with zinc concentrations up to 0.50 M. Furthermore, the study’s findings imply that less basic environments in the copper half-cell favor greater cell potentials while more basic conditions in the zinc half-cell favor higher voltages. Additionally, the study finds that through increasing the ionic strength in the reduction half-cell, the cell’s voltage can be maximized at ~1.4 V and can be modeled through a logistic growth model. This study successfully sheds light on the many factors that contribute to manipulating the applicable voltages of Zn/Cu cells.

INTRODUCTION.

Rechargeable zinc-copper batteries are currently being explored as more environmentally friendly alternatives to lithium-ion batteries in low power contexts due to a highly reversible capacity of 395 m Ah g^-1, their nearly 100% coulombic efficiency, and high energy density of 380 Wh kg^-1 [1,2]. Reversibility is an important metric to evaluate the rechargeable capacity of batteries which can be assessed alongside coulombic efficiency and energy density to substantiate the energy efficiency of these cells. The simple redox equations for zinc-copper cells are [1]:

Oxidation (Anode: Zinc):

\[Zn(s) \rightarrow\ Zn^{2+}(aq) + 2e^-\ \ \ \ \ \ \ \ \ \ \ \ \ -0.76 V\]

Reduction (Cathode: Copper):

\[Cu^{2+}(aq) + 2e^- \rightarrow\ Cu(s)\ \ \ \ \ \ \ \ \ \ \ \ \ 0.34 V\]

Based on these values, in a 1.0M Zn/1.0M Cu electrochemical cell, the expected standard cell potential would be 1.10 V (E° = E_Cathode — E_Anode). Variations of this in terms of ion concentration are understood with the Nernst equation [3]:

\[E=E°-\frac{nF}{RT}lnQ\tag{1}\]

Where Eis cell potential, E° is the standard cell potential (1.10 V) [3], n is the number of electron moles, F is Faraday’s constant, R is the ideal gas constant, T is the temperature (Kelvin), and Q is the reaction quotient.

Since for copper and zinc ions, 2 moles of electrons are transferred, and room temperature can be assumed, ~298 K, this can be simplified to:

\[E=1.10-0.0296\log{\left(Q\right)}\tag{2}\]

Reaction quotient can be expressed as the following:

\[Q=\frac{\gamma\left(Zn\right)\cdot\left[Zn\right]}{\gamma\left(Cu\right)\cdot\left[Cu\right]}\tag{3}\]

Where (γ) is the activity coefficient of X.

This study will compare the precision of the Debye Hucke and Davies equation models to determine the most effective model at specific concentration ranges for determining activity coefficient.  Activity coefficient refers to the ratio of active ions to total ions in a solution. Activity coefficients have an important implication in determining reaction quotient as demonstrated in the equation above. This information will be substituted in the Nernst equation to understand how to predict cell potential at non identical half-cell ion concentrations which will have implications in other parts of the study. It is hypothesized that increased zinc solution concentrations will correspond with decreased cell potential. At relatively low ion concentrations in its electrolytes, voltage can be mathematically modelled using the Debye Hückel Law [4]:

\[\log{\left(\gamma\right)}=\frac{-0.51i^2\cdot\sqrt I}{1+3.3\delta\cdot\sqrt I}\tag{4}\]

Where i is the ion charge, I is the ionic strength, and δ is the ion diameter (0.60 nm) [5].

Considering that for zinc and copper ions, ion diameter equals 0.60 (nm) and ion charge equals 2 in accordance with the other constants in the equation, then ionic strength can be expressed as:

\[I=\frac{1}{2}\Sigma\left(i^2\cdot M\right)\tag{5}\]

Where i is ion charge and M is molar concentration (mol L^-1). At higher concentrations, the Davies equation will be most effective for determining activity coefficients [6]:

\[\log{\left(\gamma\right)}=-0.51i^2\left(\frac{\sqrt I}{1+\sqrt I}-0.30I\right)\tag{6}\]

In addition to analyzing voltage as a function of ion concentrations, pH is another factor that can be used to influence cell potential. pH refers to how acidic or basic a substance is, in this context the electrolyte. It is hypothesized that the presence of H⁺ or OH^– ions can potentially react with the zinc or copper ions to alter their concentration which will influence cell potential. Supplementary electrolytes refer to additional highly soluble ionic compounds that are added to a solution. These can be compounds such as lithium bromide and ammonium nitrate that are highly soluble. In consequence, they can substantially influence the activity coefficients of the Zn/Cu ions and in effect alter cell potential. It is hypothesized that the addition of supplementary electrolytes to the reduction half-cell will inflate the activity coefficient values of the Cu half-cell and consequently decrease the reaction quotient and in turn increase the voltage. The research will attempt to identify the maximum experimental cell potential through this method and will discuss derived mechanisms to model this method to heighten cell potential.

MATERIALS AND METHODS.

The research methodology involved constructing a Zn-Cu cell using glassware-based containers. Newly used, ultra-corrosion-resistant grade copper and zinc metal electrodes from Thermo Fisher Scientific, polished with 400, 600, 800, and 1200 grit sandpaper, were utilized for each test. The copper and zinc electrodes were placed in the reduction and oxidation half-cells, respectively as shown in Figure 1.

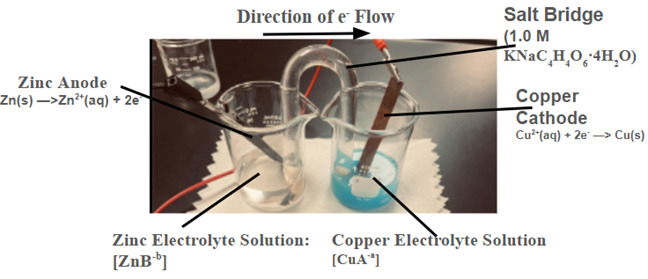
Ionic compound solutions were dispensed into the half-cells where the electrode material matched the cation of the electrolyte. Fully deionized water from Thermo Fisher Scientific was used in each half-cell. The salt bridge consisted of a glass U-tube filled with deionized water and a 1.0 M aqueous potassium sodium tartrate solution (KNaC₄H₄O₆·4H₂O). Each half-cell contained 40.0 mL of electrolyte solution with varying ion concentrations and with varying anions. Three different anions were tested: Cl^–, NO₃^–, SO₄^2-. They were bonded with their corresponding zinc/copper cations in the respective half-cell, and each chemical solution was accessed through Thermo Fisher Scientific. Each new electrolyte solution involved exchanging the half-cells for a new storage system. Seven different molarities of zinc compounds were used: 10^-3 M, 10^-1 M, 0.25 M, 0.50 M, 0.75 M, 1.0 M, and 2.0 M. As in Table 1, these were studied in conjunction with a reduction half-cell containing the copper compound with the corresponding anion maintained at a 1.0 M concentration.

Buffer solutions were used to alter the pH of the solution from neutrality. Six different pH levels were assessed: 0, 2, 6, 8, 12, and 14. pH alterations were applied to either half-cell, but not both, with pH indicators certifying the values. Both the zinc and copper half-cells were maintained at 0.001 M concentrations during pH testing. A benchtop digital multimeter (DMM) from Thermo Fisher Scientific was used to collect data on voltage (V). The addition of highly soluble ionic compounds was used (NH₄NO₃, LiBr) in the copper reduction half-cell to assess the extent to which the voltage can be increased and modeled where zinc and copper concentrations were kept at 10^-3 M and 1.0 M respectively.

RESULTS.

The concentration of the zinc ion was varied in accordance with the Nernst equation to alter cell potential and maintained at a neutral pH while the copper ion is maintained at 1.0 M for Table 1.

Table 1. Voltage versus concentration and anions
Voltage (V)	Zinc Solution Molar Concentration [M] (mol L-1)
Anion Ionically Bonded to Zn/Cu Cation		10-3	10-1	0.25	0.50	0.75	1.0	2.0
	Cl–	1.213	1.154	1.144	1.136	1.111	1.092	1.052
	NO3–	1.213	1.163	1.131	1.132	1.122	1.104	1.061
	SO42-	1.185	1.143	1.115	1.114	1.100	1.105	1.086

To examine the extent to which the voltage of the battery cell can be increased, the addition of supporting electrolytes was used. Supplementary electrolytes are additional unique ionic compounds that aim to increase the ionic strength while avoiding precipitation. Precipitation occurs when a chemical is added past the maximum solubility of its ions. Table 2 articulates the extent to which voltage was affected by this addition. Also note for Table 2, the concentration of zinc ion is kept at 10^-3 M, and the concentration of copper ion at 1.0 M. For Tables 3 and 4, the pH was varied in each half cell as labeled while the concentrations of Zn and Cu ions are kept at 10^-3 M.

Table 2. Voltage versus added secondary electrolyte concentration
Voltage (V)	Concentration of Added Ionic Species to Reduction Half Cell in Addition to 1.0M Cu(A)
Anion Ionically Bonded to Zn/Cu Cation		1.0M NH4NO3	4.0M NH4NO3	8.0M NH4NO3	12.0M NH4NO3	12.0M NH4NO3 + 16.0M LiBr
	Cl–	1.212	1.273	1.306	1.326	1.348
	NO3–	1.221	1.294	1.319	1.336	1.359
	SO42-	1.245	1.316	1.347	1.362	1.383

 

Table 3. Voltage versus pH of cathode
Voltage (V)	pH of Copper Half Cell Solution
Anion Ionically Bonded to Zn/Cu Cation		0	2	6	8	12	14
	Cl–	1.111	1.102	1.104	1.101	1.076	1.042
	NO3–	1.105	1.106	1.103	1.103	1.073	1.014
	SO42	1.104	1.107	1.102	1.105	1.054	1.025

 

Table 4. Voltage versus pH of anode
Voltage (V)	pH of Zinc Half Cell Solution
Anion Ionically Bonded to Zn/Cu Cation		0	2	6	8	12	14
	Cl–	1.033	1.072	1.107	1.102	1.137	1.187
	NO3–	1.014	1.065	1.103	1.107	1.144	1.196
	SO4	1.021	1.086	1.107	1.113	1.124	1.175

DISCUSSION.

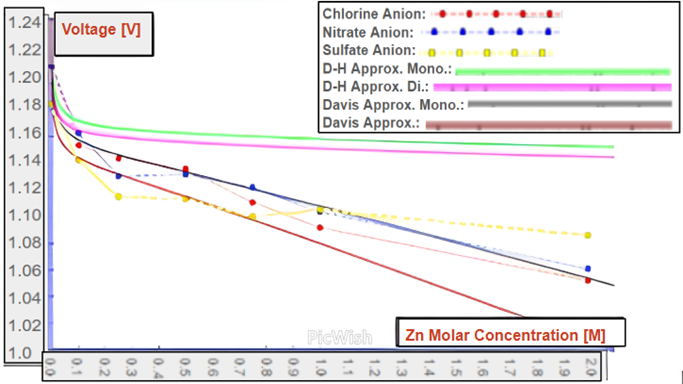
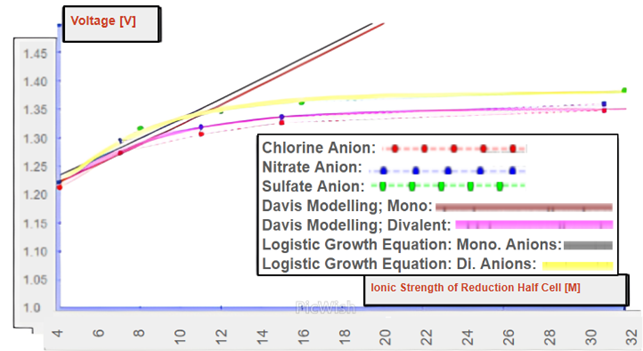
Equations were derived for low and high zinc concentrations using the Debye Hückel and Davies models respectively. These equations can be used to model cells with varying concentrations of Zn²⁺ and with varying concentrations of supplementary electrolytes. These equations were used to model the situations present in Tables 1 and 2 and are also used in the approximation curves in the graphs in Figures 2 and 3. These equations, S3 and S4, are present and discussed in more extensive detail in the Supporting Information section.

Figure 2f shows that the Debye Hückel model is effective at [Zn²⁺] less than 10^-3 M and the Davies model is effective at [Zn²⁺] less than 0.50 M. Moreover, Table 1’s data shows that divalent anionic compounds are more resistant to voltage fluctuations with changing ion concentrations than monovalent anions. The results compliment the hypothesis: higher zinc solution concentrations yielded reduced voltage.

The second graph shown, Figure 3, demonstrates that the data aligns with the hypothesis and that the addition of soluble ionic species to the copper half-cell can greatly increase the cell potential by up to 25% from the standard potential. The Davies equation remains accurate at ionic strengths less than ~10 M. Given the Davies model’s inability to model Zn/Cu cells at very high ionic strengths, logistic growth equations were developed as in equations 7 and 8. At very high ionic strengths, the logistic growth models in equation 7 approximates the cell potential for monovalent anions and the model in equation 8 approximates for divalent anions.

\[E=\frac{1.3502}{1+0.2499e^{-0.2090I}}\tag{7}\]

\[E=\frac{1.3790}{1+0.3325e^{-0.2297I}}\tag{8}\]

Each equation’s numerator (1.3502, 1.3790) approximates each cell’s maximum initial cell potentials at very high reduction cell ionic strengths.

The data from Tables 3 and 4 show that less basic environments in the copper half-cell favor greater cell potentials while more basic conditions in the zinc half-cell favor higher voltages. The interpreted chemical activity for the data is depicted in the following equations:

\[Zn(s)+2H^+(aq)\rightarrow Zn^{2+}(aq)+H_2(g)\]

\[Cu^{2+}(aq)+2OH^-(aq)\rightarrow Cu(OH)_2(s)\]

\[Zn^{2+}(aq)+2OH^-(aq)\rightarrow Zn(OH)_2(s)\]

The results complimented the hypothesis that pH affected voltage. The first chemical reaction reflects for how in more acidic conditions in the zinc cell, zinc ion concentration increased, reaction quotient increased and voltage consequently decreased by the Nernst equation; the second chemical reaction reflects how in basic conditions, copper ion concentration decreased, reaction quotient increased and cell potential thereby decreased; and the third chemical reaction shows that in basic conditions, the zinc ion concentration decreased, reaction quotient decreased and accordingly cell potential increased. Acidic conditions in the copper half-cell do not exhibit a significant effect on voltage due to copper having a lower reactivity than hydrogen ions thus projecting no thermodynamically favorable reaction to occur.

In conclusion, this paper determines the effectiveness of various physical models relative to modelling cell potential at certain concentration domains. Additionally, the paper shows how to greatly increase a cell’s voltage and how to mathematically model such using supplementary electrolytes. Furthermore, the paper describes the chemical activity present at varying pH levels in each half cell. Current research on rechargeable Zn-Cu batteries shows that techniques for adjusting cell potential are crucial for exploring the applications of these prototypes; particularly in relation to efforts to ensure they operate within suitable voltage ranges for specific uses.

ACKNOWLEDGMENTS.

I would like to thank Mr. Smirlis and Mr. Pruchyathamkorn for their support in this research.

SUPPORTING INFORMATION.

Supporting Information includes further explanations and analysis into key concepts along with a mathematical description of the Debye Hückel and Davies models that were discussed and used extensively throughout the study.

REFERENCES.

1. Zhu, Q., Cheng, M., Zhang, B., Jin, K., Chen, S., Ren, Z., Yu, Y. Realizing a rechargeable high-performance Cu–Zn battery by adjusting the solubility of Cu²⁺. Adv. Funct. Mater. 29, 1905979 (2019).
2. Xu, C., Lei, C., Li, J., He, X., Jiang, P., Wang, H. Unravelling rechargeable zinc-copper batteries by a chloride shuttle in a biphasic electrolyte. Nat. Commun. 14, 2349 (2023).
3. Beattie, G. W. Nernst’s Theory of the Concentration Cell; University of California Libraries, (1951).
4. Kielland, J. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 59, 1675–1678 (1937).
5. David Harvey. LibreTexts Chemistry 35.7: Activity Coefficients. Analytical Chemistry/Instrumental Analysis (LibreTexts)/Appendicies/35.07, (2022).
6. Davies, C. W. 397. The extent of dissociation of salts in water. Part VIII. An equation for the mean ionic activity coefficient of an electrolyte in water, and a revision of the dissociation constants of some sulphates. J. Chem. Soc. 16, 2093–2098, (1938).

---

---

Posted by buchanle on Wednesday, June 25, 2025 in May 2025.

Tags: Activity Coefficient, Battery, Electrolyte, ion, pH